[자료구조] 큐

1. 큐란?

- 스택은 나중에 들어온 데이터가 먼저 나가는 구조인데 비해 큐는 먼저 들어온 데이터가 먼저 나가는 자료구조임.

- 이러한 특성을 선입선출 (FIFO : First-In First_Out)임.

- 큐의 예시 : 놀이공원 매표소에 늘어선 대기열.

- 큐는 뒤에서 새로운 데이터가 추가되고 앞에서 데이터가 하나씩 삭제되는 구조를 말함.

- 스택은 삽입과 삭제가 같은 쪽에서 일어나지만 큐에서는 다른 쪽에서 일어남.

- 큐에서 삽입이 일어나는 곳을 후단, 삭제가 일어나는 곳을 전단이라고 함.

 

 큐의 추상 자료형

데이터 : 선입선출(FIFO)의 접근 방법을 유지하는 요소들의 모음
연산 :
init() : 큐를 초기화함.
enqueue(e) : 주어진 요소 e를 큐의 맨 뒤에 추가함.
dequeue() : 큐의 맨 앞 요소를 삭제하고 반환함.
is_empty() : 큐가 비어있으면 TRUE를 아니면 FALSE를 반환.
is_full() : 큐가 가득 차 있으면 TRUE를 아니면 FALSE를 반환함.
peek() : 큐의 맨 앞 요소를 삭제하지 않고 반환함.
size() : 큐의 모든 요소들의 개수를 반환함.

- 삽입과 삭제가 후단과 전단에서 각각 독립적으로 이루어지므로 양쪽의 위치를 기억해야함. (두개의 변수 필요)

- 삽입위치와 관련된 변수 : rear

- 삭제 위치와 관련된 변수 : front

- 큐의 연산 : enqueue() / dequeue()

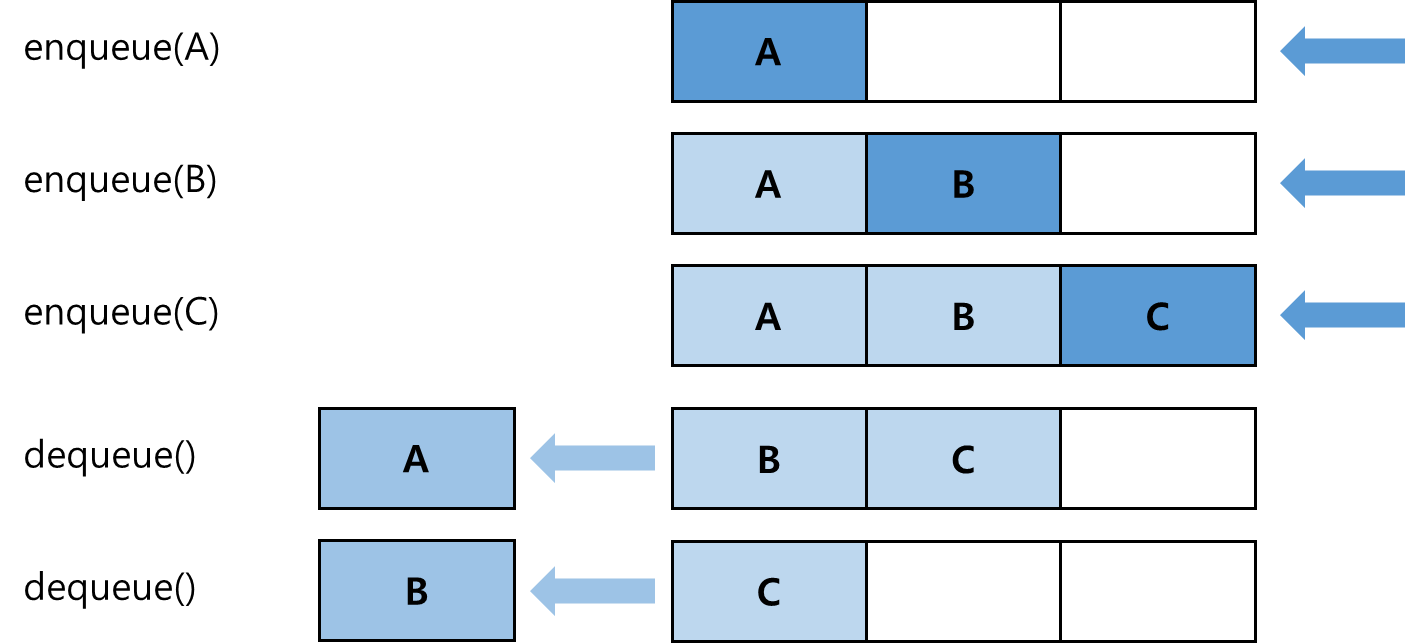
- enqueue() : 큐에 새로운 자료를 삽입하는 연산. 큐의 후단을 통해 요소를 추가함.

- dequeue() : 큐의 전단에 있는 요소를 꺼내서 반환함.

 

 

큐의 활용

- 일상생활에서 대부분의 일들이 먼저 들어온 순서대로 처리되는 것과 같이 컴퓨터에서도 큐는 매우 광범위하게 사용됨.

- 컴퓨터 장치들 사이에서 데이터를 주고받을 때 각 장치들 사이에 존재하는 속도의 차이나 시간차이를 극복하기 위한 임시 기억 장치로 큐가 사용됨. => 버퍼

 

버퍼링의 개념

- 대부분의 장치에서 발생하는 이벤트는 불규칙적으로 발생함. 이에 비해 CPU와 같이 발생한 이벤트를 처리하는 장치는 일정한 처리 속도를 가지고 있음.

- 이 둘 사이의 속도 차이를 버퍼를 사용하여 해결함.

- 키보드와 컴퓨터 사이에 큐(입력 버퍼)가 필요함. 컴퓨터가 다른 작업을 하고 있는 순간에 사용자가 키보드로 타이핑하더라도 입력된 키 정보를 잃어버리지 않아야 하므로 입력 버퍼에 저장함. 이것은 컴퓨터가 하던 작업을 끝낸 후 순서대로 가져가서 처리함.

- 컴퓨터와 프린터 사이에 인쇄 작업 큐가 존재함. 프린터는 CPU에 비해 상대적으로 속도가 느림. CPU가 빠른 속도로 인쇄 데이터를 만들고, 이것을 인쇄 작업 큐에 저장한 후 다른 작업으로 넘어감.

- 실시간 비디오 스트리밍에서 다운로드 된 데이터가 비디오를 재생하기에 충분하지 않으면 순서대로 모아두었다가 충분한 양이 되었을 때 비디오를 복원하여 재생함. => 버퍼링

- 컴퓨터를 이용해 시뮬레이션 하는 분야에서도 이용됨. 은행에서 대기표를 뽑고 기다리는 고객들, 인터넷에서 전송되는 데이터 패킷들을 모델링하는데 큐가 이용됨.

 

2. 배열을 이용한 큐

선형 큐

배열로 정수를 저장할 선형 큐를 구현하기 위해 정수의 1차원 배열을 선언함.

삽입과 삭제 연산을 위한 변수가 있어야함. 삭제를 위한 변수로 큐의 첫번째 요소를 가리키는 변수를 front로 정의함. 삽입을 위한 변수로 큐의 마지막 요소를 가리키는 변수를 rear라고 정의함.

- 이해하기 쉽지만 front와 rear값이 증가만 한다는 문제가 있음 => 배열의 앞부분이 비어있더라도 삽입하지 못함.

- 후단에 삽입할 공간이 없으면 요소들을 왼쪽으로 옮겨야하지만 매우 번거롭고 비효율적임.

 

=> 이 문제를 해결하기 위해 배열을 선형이 아닌 원형으로 생각함.

 

원형 큐

- front와 rear의 값이 배열의 끝에 도달하게 되면 그 다음에 증가되는 값은 0이 되도록 함.

- 배열의 처음과 끝이 원형으로 연결되어 있다고 생각하면 됨.

- 원형큐의 초기값은 front와 rear가 같은 위치를 가리킴.

 

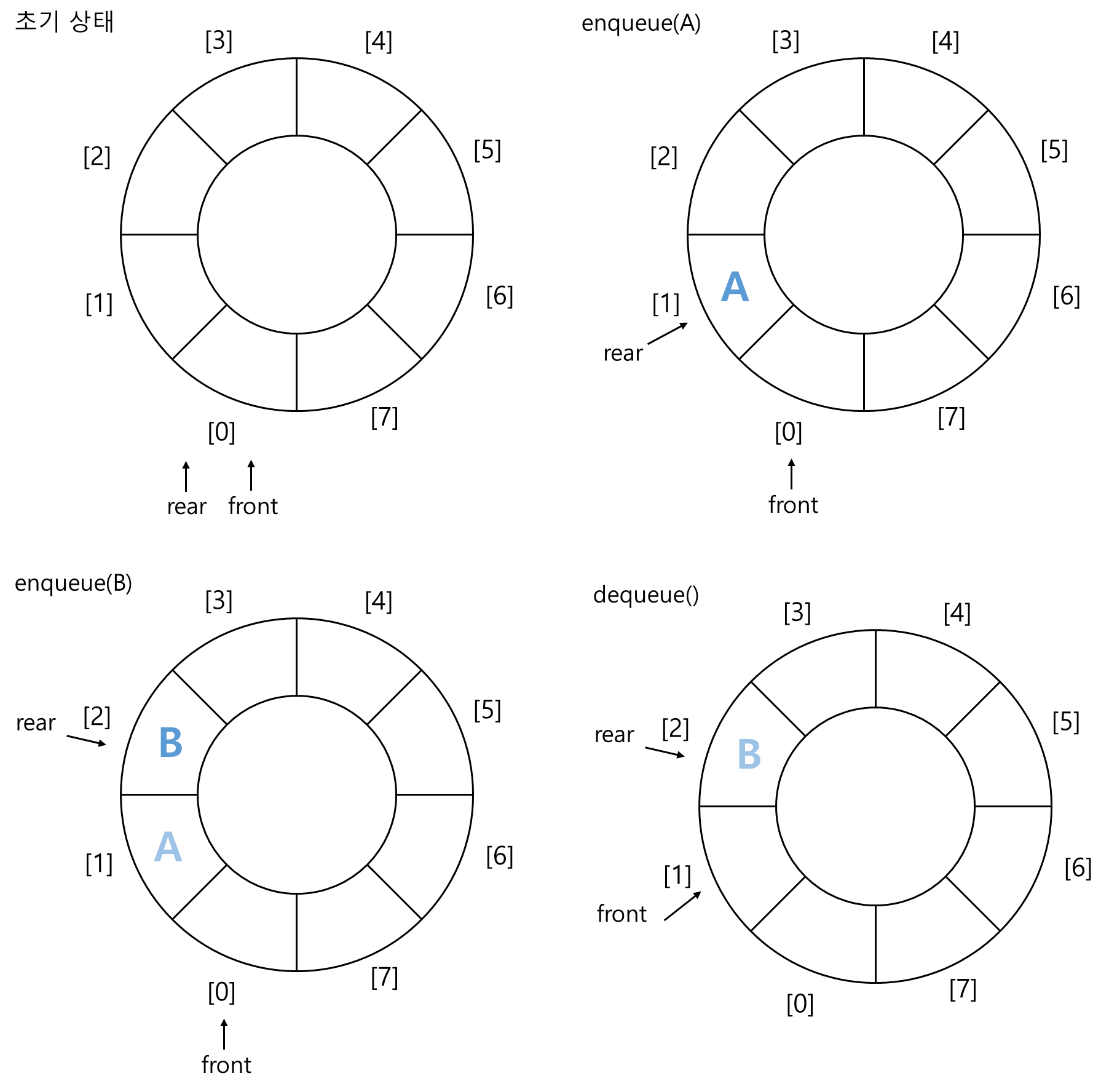
공백 상태와 포화 상태

- front와 rear의 값이 같으면 공백 상태이고, 만약 front가 rear보다 하나 앞에 있으면 포화 상태가 됨.

- 큐의 요소들의 개수를 관리하는 추가적인 변수를 사용한다면 한 자리를 비워두지 않아도 됨.

 

큐의 is_empty() 연산

is_empty()

if front  =rear
    then return TRUE
    else return FALSE

 

큐의 is_full() 연산

is_full()

if front = (rear+1) % MAX_QUEUE_SIZE
    then return TRUE
    else return FALSE

 

삽입과 삭제 연산

- 삽입이나 삭제 전에 먼저 front와 rear를 원형 회전시켜서 하나 증가시키고 증가된 위치에 데이터를 삽입하거나 삭제해야함.

- 원형으로 회전시키기 위해 나머지 연산자 %를 사용함.

front <- ( front + 1) % MAX_QUEUE_SIZE;

rear <- ( rear +1 ) % MAX_QUEUE_SIZE;

 

원형큐에서의 삽입 알고리즘

enqueue(x)

if is_full()
    then error "overflow"
    else rear <- (rear+1) % MAX_QUEUE_SIZE;
        data[rear] <- x;

 

원형큐에서의 삭제 알고리즘

dequeue()

if is_empty()
    then error "underflow"
    else rear <- (front+1) % MAX_QUEUE_SIZE;
        return data[front];

 

초기화와 요소의 개수 검사

- 초기화는 공백상태로 만드는 것을 의미하므로 front와 rear를 동일한 값으로 설정함.

- 항목의 개수는 rear가 회전되어 front와 역전되면 음수가 되어 문제 발생함.

- 여기에 전체 항목의 수를 더한 값이 항목의 개수가 됨 -> 전체 항목의 수를 더한 후 전체 항목의 수의 나머지를 구함.

 

원형 큐의 초기화

init()

front = 0;
rear = 0;

 

원형 큐의 요소의 개수

size()

return (rear-front + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;

 

3. 원형 큐의 구현

- 스택과 같이 큐를 위한 데이터( data[] ), front, rear는 전역 변수로 선언하고, 연산들은 함수로 구현함.

- 원형큐에 필요한 front와 rear는 int형으로 선언함.

- 스택에서와 같이 큐 항목의 자료형을 Element라 하면, data는 Element형 배열이 됨.

 

원형 큐 프로그램 구현 결과 및 코드

전체 코드 보기

#include <stdio.h>
#include <stdlib.h>
#define MAX_QUEUE_SIZE 100

typedef int Element;
Element data[MAX_QUEUE_SIZE];
int front;
int rear;

void error(char msg[])
{
	printf("%s\n", msg);
	exit(1);
}
void init_queue() { front = 0; rear = 0; }
int is_empty() { return front == rear; }
int is_full() { return front == (rear + 1) % MAX_QUEUE_SIZE; }
int size() { return (rear - front + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE; }

void enqueue(Element e)
{
	if (is_full())
		error("큐 포화상태 에러");
	else
	{
		rear = (rear+1)%MAX_QUEUE_SIZE;
		data[rear] = e;
	}
}
Element dequeue()
{
	if (is_empty())
		error("큐 공백상태 에러");
	else
	{
		front = (front + 1) % MAX_QUEUE_SIZE;
		return data[front];
	}
}
Element peek()
{
	if (is_empty())
		error("큐 공백상태 에러");
	else
	{
		return data[(front + 1) % MAX_QUEUE_SIZE];
	}
}

void print_queue(char msg[])
{
	int m = rear;
	if (front >= rear)
		m += MAX_QUEUE_SIZE;
	printf("%s[%2d]= ", msg, size());
	for (int i = front + 1; i <= m; i++)
		printf("%2d ", data[i % MAX_QUEUE_SIZE]);
	printf("\n");
}

int main()
{
	init_queue();
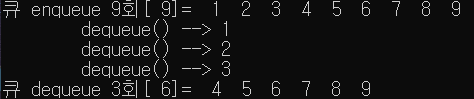
	for (int i = 1; i < 10; i++)
		enqueue(i);
	print_queue("큐 enqueue 9회");
	printf("\tdequeue() --> %d\n", dequeue());
	printf("\tdequeue() --> %d\n", dequeue());
	printf("\tdequeue() --> %d\n", dequeue());
	print_queue("큐 dequeue 3회");

	return 0;
}

 

4. 덱이란?

- 덱은 double-ended queue의 줄임말로서 큐의 전단(front)과 후단(rear)에서 모두 삽입과 삭제가 가능한 큐를 의미함.

- 중간에 삽입하거나 삭제하는 것은 허용하지 않음.

 

덱의 추상 자료형

데이터 : 전단과 후단을 통한 접근을 허용하는 요소들의 모음
연산 :
init() : 덱을 초기화함.
add_front(e) : 주어진 요소 e를 덱의 맨 앞에 추가함.
delete_front() : 전단 요소를 삭제하고 반환함.
add_rear(e) : 주어진 요소 e를 덱의 맨 뒤에 추가함.
delete_rear() : 후단 요소를 삭제하고 반환함.
get_front() : 전단 요소를 삭제하지 않고 반환함.
get_rear() : 후단 요소를 삭제하지 않고 반환함.
is_empty() : 공백 상태이면 TRUE 아니면 FALSE를 반환함.
is_full() : 덱이 가득 차 있으면 TRUE 아니면 FALSE를 반환함.
size() : 덱 내의 모든 요소들의 개수를 반환함.

- 덱은 스택과 큐의 연산들을 모두 가지고 있음.

- add_front와 delete_front연산은 스택의 push와 pop 연산과 동일함.

- add_rear연산과 delete_front 연산은 각각 큐의 enqueue와 dequeue연산과 동일함.

- 추가로 덱은 get_front, get_rear, delete_rear연산을 가짐.

- 덱은 스택이나 큐에 비해 더 융통성이 많은 자료구조임.

 

배열을 이용한 원형 덱

- 원형 큐를 확장하면 원형 덱도 손쉽게 구현할 수 있음.

- 큐에서 사용한 배열 data와 front, rear를 그대로 사용하면 됨.

- is_empty(), is_full(), size() 연산은 이름과 동작이 모두 동일함.

- 덱에서 추가된 연산은 delete_rear(), add_front(), get_rear()가 있고, 이외에는 알고리즘이 정확히 동일함.

 

- delete_rear()와 add_front()에서는 원형 큐에서와 다르게 반대방향의 회전이 필요함. front나 rear를 감소 시켜야 하는데, 만약 음수가 되면 MAX_QUEUE_SIZE를 더해주어야 함.

front <- (front-1 + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;

rear <- (rear-1 + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;

 

5. 덱의 구현

- 원형 덱은 큐의 코드를 이용하면 쉽게 구현할 수 있음.

 

추가된 함수

add_front 함수

void add_front(Element e)
{
	if (is_full())
		error("덱 포화상태 에러");
	else
	{
		data[front] = e;
		front = (front - 1 + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;
		
	}
}

 

del_rear 함수

Element del_rear()
{
	if (is_empty())
		error("덱 공백상태 에러");
	else
	{
		int r = rear;
		rear = (rear - 1 + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;
		return data[r];
	}
}

 

peek_rear 함수

Element peek_rear()
{
	if (is_empty())
		error("덱 공백상태 에러");
	else
		return data[rear];
}

 

원형 덱 프로그램 구현 결과 및 코드

전체 코드 보기

#include <stdio.h>
#include <stdlib.h>
#define MAX_QUEUE_SIZE 100

typedef int Element;
Element data[MAX_QUEUE_SIZE];
int front;
int rear;

void error(char msg[])
{
	printf("%s\n", msg);
	exit(1);
}
void init_dequeue() { front = 0; rear = 0; }
int is_empty() { return front == rear; }
int is_full() { return front == (rear + 1) % MAX_QUEUE_SIZE; }
int size() { return (rear - front + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE; }

void add_rear(Element e)
{
	if (is_full())
		error("덱 포화상태 에러");
	else
	{
		rear = (rear+1)%MAX_QUEUE_SIZE;
		data[rear] = e;
	}
}
void add_front(Element e)
{
	if (is_full())
		error("덱 포화상태 에러");
	else
	{
		data[front] = e;
		front = (front - 1 + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;
		
	}
}
Element del_front()
{
	if (is_empty())
		error("덱 공백상태 에러");
	else
	{
		front = (front + 1) % MAX_QUEUE_SIZE;
		return data[front];
	}
}

Element del_rear()
{
	if (is_empty())
		error("덱 공백상태 에러");
	else
	{
		int r = rear;
		rear = (rear - 1 + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;
		return data[r];
	}
}

Element peek_front()
{
	if (is_empty())
		error("덱 공백상태 에러");
	else
	{
		return data[(front + 1) % MAX_QUEUE_SIZE];
	}
}

Element peek_rear()
{
	if (is_empty())
		error("덱 공백상태 에러");
	else
		return data[rear];
}

void print_queue(char msg[])
{
	int m = rear;
	if (front >= rear)
		m += MAX_QUEUE_SIZE;
	printf("%s[%2d]= ", msg, size());
	for (int i = front + 1; i <= m; i++)
		printf("%2d ", data[i % MAX_QUEUE_SIZE]);
	printf("\n");
}

int main()
{
	init_dequeue();
	for (int i = 1; i < 10; i++)
		add_rear(i);

	for (int i = 2; i <=6; i += 2)
		add_front(i);
	print_queue("덱 삽입 12회");
	printf("\tdel_front() --> %d\n", del_front());
	printf("\tdel_front() --> %d\n", del_front());
	printf("\tdel_rear() --> %d\n", del_rear());
	printf("\tdel_rear() --> %d\n", del_rear());
	print_queue("덱 삭제 4회");

	return 0;
}

 

연결된 덱의 구현

- 덱도 연결 리스트로 구현할 수 있지만 스택이나 큐에 비해 더 복잡함.

- 하나의 노드에 선행 노드와 후속노드를 가리키는 포인터 변수를 가져야함 -> 이러한 구조를 이중 연결 리스트라고 부름.

 

6. 큐의 응용 : 은행 시뮬레이션

시뮬레이션과 큐잉이론

- 시뮬레이션 : 모의실험을 의미함. 어떤 일을 실행하기에 앞서서 프로그램을 이용하여 가상으로 실험해 보고 처리 과정과 결과를 미리 분석해 보는 것을 말함. 시뮬레이션 하기 위해서 주어진 시스템을 수학적으로 모델링해야함.

- 이러한 모델링에 사용되는 통계적 이론을 큐잉이론이라 함.

- 어떤 시스템을 컴퓨터를 이용하여 큐잉이론에 따라 시뮬레이션 하고, 시스템의 특성을 분석하는 데 이용함.

- 보통 고객에 대한 서비스를 수행하는 서버와 서비스를 받는 고객들로 이루어짐.

 

은행 서비스 시뮬레이션

- 은행 창구는 하나라고 가정함.

- 고객들은 순서대로 서비스를 받으며, 한 고객의 서비스가 끝나면 다음 고객이 서비스를 받음.

- 시뮬레이션 할 최대 시간

- 단위시간에 도착하는 고객 수

- 한 고객에 대한 최대 서비스 시간

- 고객들은 단위시간에 도착하는 고객 수를 바탕으로 무작위로 발생됨. 서비스 시간도 최대 시간 내에서 무작위로 결정됨.

 

시뮬레이션 구현

- 고객의 정보를 정의하기 위해 고객의 번호, 도착 시간, 서비스에 필요한 시간 등이 있어야 하기 때문에 Customer 구조체를 정의해 사용함.

typedef struct Customer {
	int id;
	int time;
	int service_time;
}Customer;

 

-큐에 저장할 데이터가 Customer이므로 Element를 지정함.

typedef Customer Element;

- read_sim_params() : 시뮬레이션 파라미터를 사용자로부터 읽는 함수.

- insert_customer() : 새로운 고객이 들어온 경우에 대한 처리 함수.

run_simulation() : 시뮬레이션 주 함수

전체 코드 보기

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include  <stdlib.h>
#include <time.h>
#define MAX_QUEUE_SIZE 100

typedef struct Customer {
	int id;
	int time;
	int service_time;
}Customer;

typedef Customer Element;
Element data[MAX_QUEUE_SIZE];
int front;
int rear;

void error(char msg[])
{
	printf("%s\n", msg);
	exit(1);
}
void init_queue() { front = 0; rear = 0; }
int is_empty() { return front == rear; }
int is_full() { return front == (rear + 1) % MAX_QUEUE_SIZE; }
int size() { return (rear - front + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE; }

void enqueue(Element e)
{
	if (is_full())
		error("덱 포화상태 에러");
	else
	{
		rear = (rear + 1) % MAX_QUEUE_SIZE;
		data[rear] = e;
	}
}

Element dequeue()
{
	if (is_empty())
		error("덱 공백상태 에러");
	else
	{
		front = (front + 1) % MAX_QUEUE_SIZE;
		return data[front];
	}
}

Element peek()
{
	if (is_empty())
		error("덱 공백상태 에러");
	else
	{
		return data[(front + 1) % MAX_QUEUE_SIZE];
	}
}

int nSimulation; // 시뮬레이션 시간
double probArrival; // 평균 고객 수
int tMaxService; // 최대 서비스 시간
int totalWaitTime; // 최대 기다리는 시간
int nCustomers; //전체 고객의 수
int nServedCustomers; // 서비스를 받은 고객의 수

double rand0to1() { return rand() / (double)RAND_MAX; }

void insert_customer(int arrivalTime)
{
	Customer c;
	c.id = ++nCustomers;
	c.time = arrivalTime;
	c.service_time = (int)(tMaxService * rand0to1()) + 1;
	printf("고객 %d 방문 ( 서비스 시간 : %d분)\n", c.id, c.service_time);
	enqueue(c);
}

void read_sim_params()
{
	printf("시뮬레이션 할 최대 시간 (예:10) = ");
	scanf("%d", &nSimulation);
	printf("단위시간에 도착하는 고객 수 (예:0.5) = ");
	scanf("%lf", &probArrival);
	printf("한 고객에 대한 최대 서비스 시간 (예:5) = ");
	scanf("%d", &tMaxService);
	printf("======================================\n");
}

void run_simulation()
{
	Customer c;
	int clock = 0;
	int serviceTime = -1;

	init_queue();
	nCustomers = totalWaitTime = nServedCustomers = 0;

	while (clock < nSimulation) {
		clock++;
		printf("현재시각=%d\n", clock);

		if (rand0to1() < probArrival)
			insert_customer(clock);
		if (serviceTime > 0) serviceTime--;
		else {
			if (is_empty()) continue;
			c = dequeue();
			nServedCustomers++;
			totalWaitTime += clock + c.time;
			printf(" 고객 %d 서비스 시작 (대기시간:%d분)\n",c.id,clock-c.time);
			serviceTime = c.service_time - 1;
		}
	}
}

void print_result()
{
	printf("===============================================\n");
	printf(" 서비스 받은 고객수 = %d\n", nServedCustomers);
	printf(" 전체 대기 시간     = %d\n", totalWaitTime);
	printf(" 서비스고객 평균대기시간 = %-5.2f분\n",(double)totalWaitTime / nServedCustomers);
	printf(" 현재 대기 고객수 = %d\n", nCustomers - nServedCustomers);
}
int main()
{
	srand((unsigned int)time(NULL));
	read_sim_params();
	run_simulation();
	print_result();

	return 0;
}

7. 덱의 응용 : 미로 탐색 프로그램

- 미로에서 출구를 찾기 위해 다양한 탐색 방법을 사용할 수 있음.

- 가장 간단한 탐색 방법은 시행착오를 이용하는 것으로 하나의 경로를 선택하여 시도해 보고 막히면 다시 다른 경로를 시도하는 것.

- 이때 현재의 경로가 막혔을 때 다시 선택할 수 있는 다른 경로들을 어딘가에 저장해야함.

- 그래프 탐색에서는 대표적인 두가지 방법이 있음

깊이 우선 탐색(DFS, Depth First Search) 전략 : 가장 최근에 저장된 경로를 순서대로 선택하여 시도하는 방법. 스택을 이용해 구현함.
너비 우선 탐색(BFS, Breadth First Search) 전략 : 가장 먼저 저장된 경로를 선택하여 시도하는 방법. 큐를 이용해서 구현함.

- 현재 위치에서 갈 수 있는 방들의 좌표를 저장함. 막다른 길을 만나면 가장 최근에 저장한 아직 가보지 않은 방으로부터 새로운 경로를 시작함.

- 한번 가본 방은 다시 가면 안됨. -> 무한 루프에 빠지면 안되기 때문

- 방을 지나갈 때마다 표시를 해서 닷 ㅣ가지 않도록 해야함.

- 현재 위치가 출구가 아니면 이동이 가능한 이웃(상하좌우) 칸의 위치를 저장함. 다음으로 하나의 위치를 꺼내 현재의 위치로 설정하고, 같은 작업을 반복함.

- 반복은 현재의 위치가 출구와 같거나 더 이상 갈 수 있는 위치가 없을 때까지 계속됨.

 

미로 탐색 알고리즘

- 모든 위치는 (행, 열)로 표시함. 입구 위치를 스택 또는 큐에 넣어주면 탐색이 시작됨.

- 하나의 위치를 꺼내 탐색하는 과정을 반복함. 만약 스택이 공백상태이면 미로에는 출구가 없음.

- 현재 위치(r,c)가 출구이면 탐색은 성공으로 끝남. 그렇지 않으면 현재 위치의 이웃인 위, 아래,왼쪽, 오른쪽 방을 살펴봄.

- 만약 이 방이 방문되지 않았고, 갈 수 있는 방이라면 그 방의 위치를 모두 삽입함.

- 너비 우선 탐색은 스택을 큐로 바꾸면 됨.

 

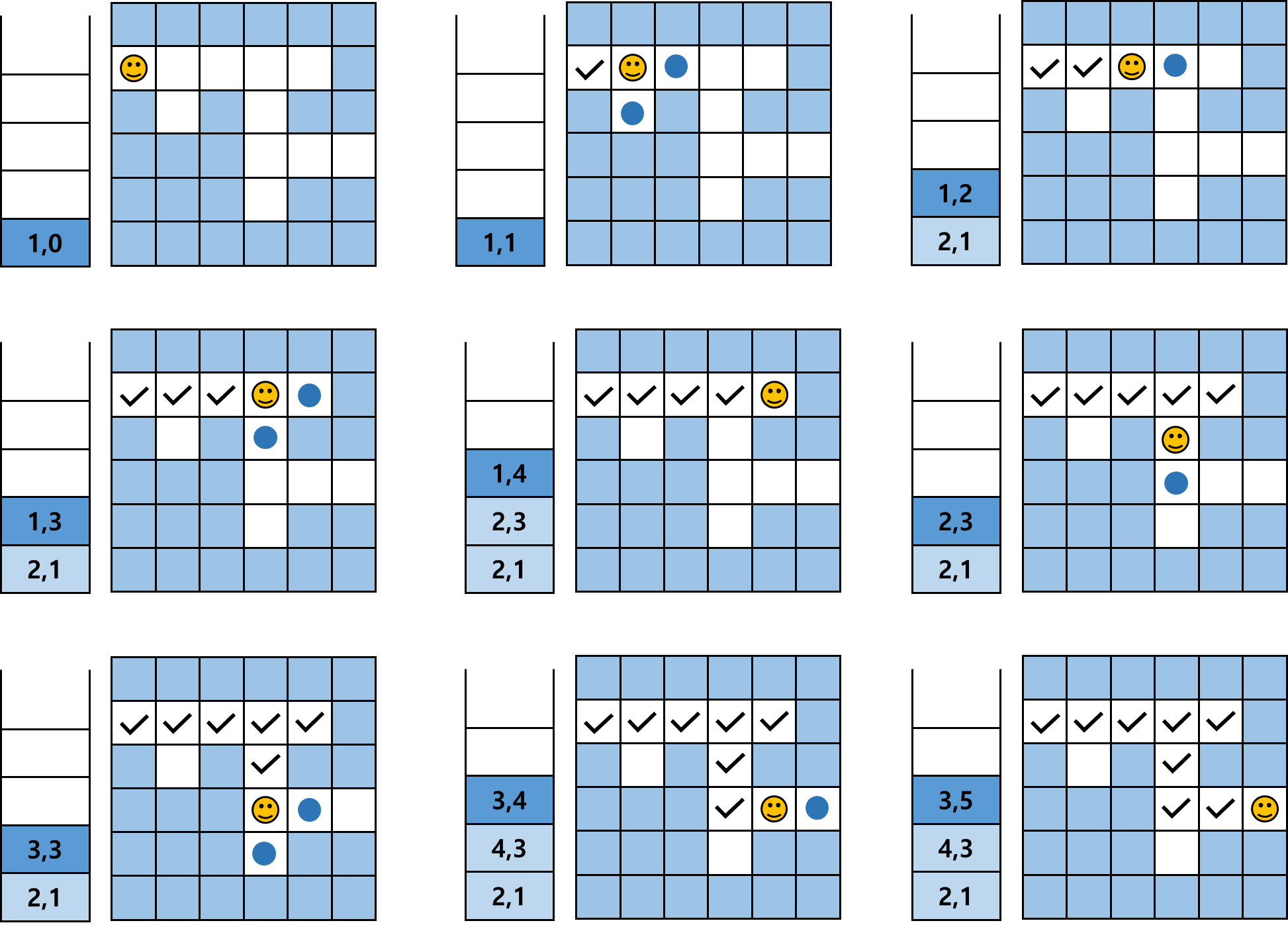
depth_first_search()

스택과 출구의 위치 x를 초기화;
스택에 입구의 위치를 삽입;
while( is_empty() = false )
    do 현재위치 <-pop();
         if( 현재 위치가 출구이면 )
            then 성공;
         if ( 현재위치의 위, 아래, 왼쪽, 오른쪽 방이 아직 방문되지 않았고 갈 수 있으면 )
            then 그 위치들을 스택에 push();
실패;

 

덱을 이용한 미로 탐색 알고리즘의 구현

- 위치를 덱에 저장하기 위한 구조체가 필요함.

typedef struct{
    int x;
    int y;
}Location;

- 미로 맵은 2차원 char 배열을 이용함. 배열에서 '0'은 갈 수 있는 방을 나타내고, 'e'와 'x'는 입구와 출구를 나타냄. 

- 한번 지나간 방은 '.' 표시를 하여 지나갔음을 나타냄.

 

미로탐색 알고리즘 구현 결과 및 코드

 

1. 깊이 우선 탐색

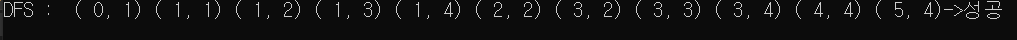
코드 보기

int DFS()
{
	int x, y;
	Location here;

	init_dequeue();
	add_rear(getLocation(0, 1));
	printf("DFS : ");

	while (is_empty() == 0)
	{
		here = del_rear();
		printf(" (%2d,%2d)", here.x, here.y);
		x = here.x;
		y = here.y;
		if (map[y][x] == 'x')return 1;
		else {
			map[y][x] = '.';
			if (is_valid(x - 1, y)) add_rear(getLocation(x-1, y));
			if (is_valid(x + 1, y)) add_rear(getLocation(x + 1, y));
			if (is_valid(x , y- 1)) add_rear(getLocation(x , y- 1));
			if (is_valid(x, y + 1)) add_rear(getLocation(x, y + 1));
		}
	}
	return 0;
}

 

2. 너비 우선 탐색

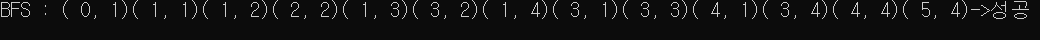
전체 코드 보기

int BFS()
{
	int x, y;
	Location here;

	init_dequeue();
	add_rear(getLocation(0, 1));
	printf("BFS : ");

	while (is_empty() == 0)
	{
		here = del_front();
		printf("(%2d,%2d)", here.x, here.y);
		x = here.x;
		y = here.y;
		if (map[y][x] == 'x')return 1;
		else {
			map[y][x] = '.';
			if (is_valid(x - 1, y)) add_rear(getLocation(x - 1, y));
			if (is_valid(x + 1, y)) add_rear(getLocation(x + 1, y));
			if (is_valid(x, y - 1)) add_rear(getLocation(x, y - 1));
			if (is_valid(x, y + 1)) add_rear(getLocation(x, y + 1));
		}
	}
	return 0;
}