[알고리즘] 선택 알고리즘

1. 평균 선형 시간 선택 알고리즘

- 퀵 정렬처럼 분할한 후 자기호출 방법을 쓰면 평균적으로 선형 시간에 i번째 작은 원소를 찾을 수 있음. 그렇지만 이 알고리즘은 최악의 경우 O(n²) 시간이 소요됨.

- 이번 알고리즘은 단점을 개선해서 최악의 경우에도 선형 시간에 i번째 작은 원소를 찾을 수 있게 함.

 

- n개의 원소가 규칙 없이 저장된 배열에서 i번째 작은 원소를 찾으려 함.

- 분할 알고리즘이 리턴하는 값으로 기준 원소가 전체에서 몇 번째 작은 원소인지 알 수 있음.

- 기준원소가 전체에서 k번째 작은 원소란 사실을 알면, i와 k의 값을 비교해서 작으면 왼쪽 그룹에 있는 원소 중 하나이고, 같으면 기준 원소가 바로 i번째 작은 수이고, 크면 i 번째 작은 수는 오른쪽 그룹에 있는 원소 중 하나임.

 

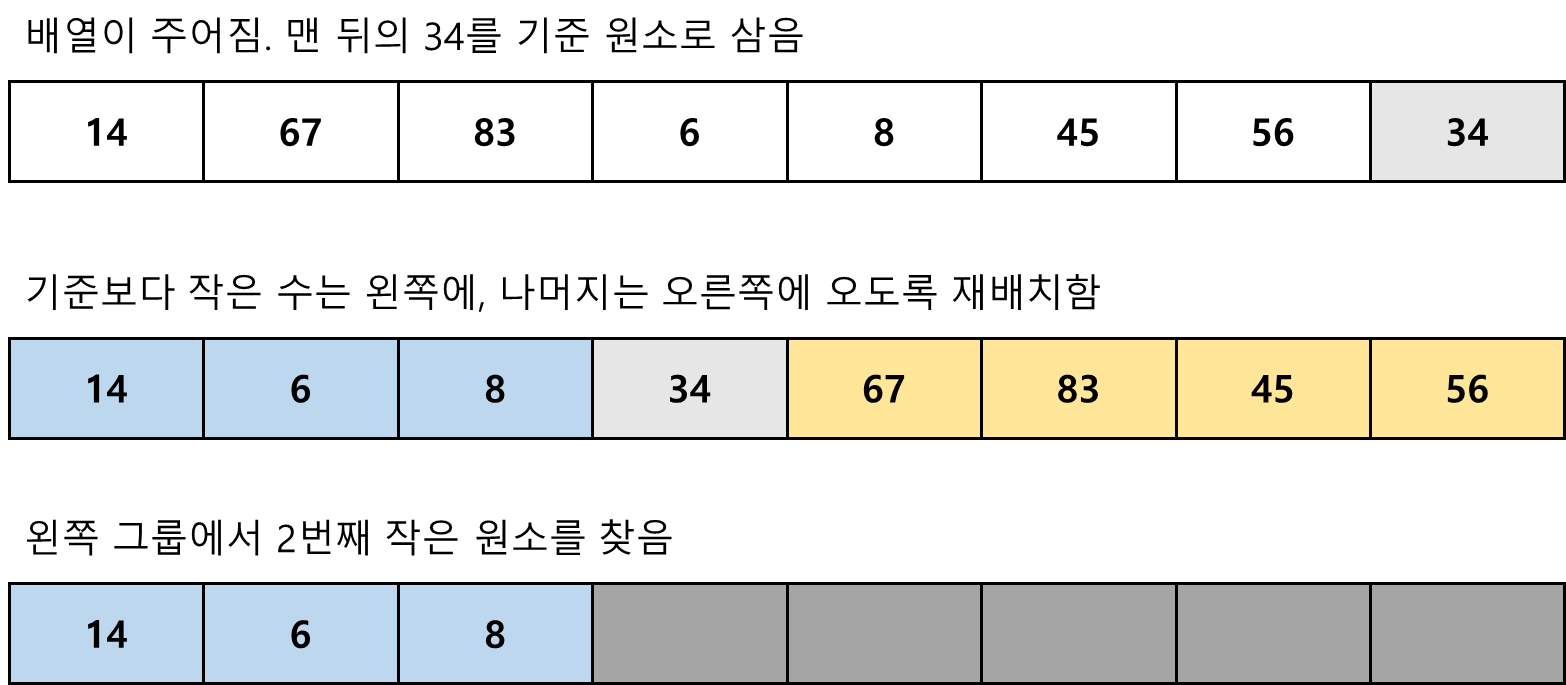
2번째 작은 원소를 찾는 예

 

7번째 작은 원소를 찾는 예

select(A, p, r, i )
{
    if (p = r ) then return A[p];
    q <- partition( A, p, r);
    ① k <- q-p + 1;
    if ( i < k ) then return select ( A, p, q-1, i);
    else if ( i = k ) then return A[q];
    else return select(A, q+1, r, i-k);
}

- ①을 통해 기준원소가 전체에서 k번째 작은 원소. i와 k를 비교해서 각 그룹을 대상으로 자기호출 함.

 

이 알고리즘의 수행 시간

- 기준원소가 전체 집합에서 k번째 작은 원소이면 두 그룹은 각각 k-1개와 n-k개로 나뉨.

T(n) ≤ max[T(k-1),T(n-k)] + θ(n)

- 평균적인 경우 θ(n) 시간이 걸리지만 최악의 경우에는θ(n²)의 시간이 소요됨.

 

2. 최악의 경우에도 선형 시간을 보장하는 선택 알고리즘

linearSelect(A, p, r, i)
{
    1. 원소의 총수가 5개 이하이면 i번째 원소를 찾고 알고리즘을 끝냄
    2. 전체 원소를 5개씩의 원소를 가진 n/5개의 그룹으로 나눔.
    3. 각 그룹에서 중앙값을 찾음.
    4. 여러 중앙값을 재귀적으로 구함. 원소의 총수가 홀수면 중앙값이 하나, 짝수면 두개중 임의로 선택함.
    5. 중앙값을 기준원소로 삼아 전체 원소를 분할함.
    6. 분할된 두 그룹중 적합한 쪽을 선택해 재귀적으로 반복함.
}