- C
- app
- 리눅스마스터2급
- Unix_System
- codingTest
- kubeflow
- study
- c++
- Algorithm
- 오블완
- Linux
- 자격증
- Java
- SingleProject
- 티스토리챌린지
- Personal_Study
- tensorflow
- Operating_System
- Baekjoon
- Artificial_Intelligence
- Univ._Study
- Python
- Database_Design
- Image_classification
- programmers
- Kubernetes
- datastructure
- Android
- cloud_computing
- 2023_1st_Semester
코딩 기록 저장소
[23-01/인공지능] 문제해결 및 탐색전략 - 1 본문
1. 문제해결 (Problem Solving)
문제해결이란?
- 초기 상태(state)에서 목표 상태(goal state)에 도달하는 과정
- 8-Puzzle 문제
- 타일을 1부터 8까지 순서대로 배치해야 함
- 문제를 해결하려면 어떻게 해야하나?

Example : Romania
- Romania에서 휴가를 보내고 내일 Bucharest라는 도시로 돌아가서 비행기를 타고자 함
- 현재 Arad라는 도시에 있다면, 어떻게 Bucharest까지 갈 수 있을까?

■ 초기 상태, 목표 상태 설정
- 초기 상태: Arad / 목표 상태 : Bucharest
■ 문제 정의
- 상태(state) : 도시(various cities)
- 동작(action) : 운전을 통해 도시 사이를 이동
■ 문제의 해 (solution)
- Sequence of Cities (여러 개의 action을 통해 도시를 돌아다니면서 Bucharest까지 가는 경로)
- e.g. Arad, Sibiu, Fagaras, Bucharest
■ 상태 공간(state space)으로 부터 최적의 문제의 해(optimal solution)를 찾아야 함
- 즉 초기 상태(initial state)에서 목표 상태(goal state)에 도달할 수 있는 모든 경로들의 집합으로부터 최적의 요소(element)를 찾아야함
- 최적의 문제의 해 → 여기서는 최단거리(경로)로 이동하는 것
2. 상태 공간과 탐색 (State Space and Search)
탐색 (Search)
- 문제의 해(solution)이 될 수 있는 것들의 집합을 상태 공간(state space)로 간주하고, 문제에 대한 최적의 해(Optimal solution)을 찾기 위해 공간을 체계적으로 찾아 보는 것
- 상태(state) : 특정 시점에 문제가 처해있는 모습
- 초기상태(initial state) : 문제가 주어진 시점의 시작 상태
- 목표 상태(goal state) : 문제가 원하는 최족 상태
- 동작(Action) : 상태의 변화 (특정 상태에서 다른 상태로의 움직이는 행동)
- 상태공간(state space) : 문제해결 과정 중 초기상태에서 목표상태에 도달 할 수 있는 모든 상태들의 집합 (즉 문제의 해가 될 수 있는 모든 상태들의 집합)
- 해공간(solution space) : (목표상태가 여러 개일 경우) 모든 목표 상태의 집합
문제해결과정 : 초기상태에서 출발하여 목표상태에 도달하는 경로(또는 연산자들의 순서)
→ 이러한 해결과정을 찾는 것이 "탐색(Search)"
문제의 형식화 (Problem Formulation)
- 인공지능을 통해 기계적으로 문제를 탐색하기 위해서는 문제에 대한 형식화가 필요
- Machine-based Search를 통해 최적의 문제의 해를 찾기 위한 4가지 구성요소 (4 Components)

ⓛ 초기 상태 정의
→ 어디서 또는 어느 상태(state)에서 시작하는지 정의
( e.g. S(Arad) )
② 가능한 동작(action) 정의
→ successor_fn(x) : successor 함수
- x라는 input을 받으면, (action,successor)라는 pair가 output으로 return되는 함수
( e.g. S(Arad) = { (Arad → Zerind, Zerind), .. } )
- 즉, Arad에서 Zerind라는 도시로 action을 통해 움직이면, successor(후임) state인 Zerind로 도달
③ 목표 도달 확인 (Goal Test)
→ 가능한 동작을 통해 목표 상태에 도달하였는지 확인
- x라는 input이 Bucharest인지 확인
( e.g. x = 'Bucharest' - Explicit : 명시적으로 확인, Checkmate(x) - Implicit : 암시적(함수이용) 확인 )
④ 경로 비용 (Path cost) 확인
→ 어떤 state에서 action을 취해 다른 state로 가는 것을 경로(path)라고 하며, 이때 드는 비용이 path cost
- step cost c(x, a, y) ≥ 0 : x라는 state에서 a라는 action을 통해 y라는 state에 도달할 때의 비용 c
인공지능에서는 초기상태에서 목표상태에 도달하는 수많은 action에서 최적의 action (optimal solution)을 (형식화 표현을 기반으로) 자동적으로 찾아내는 과정을 목표로 함
상태공간의 선택 (Selecting a State Space)
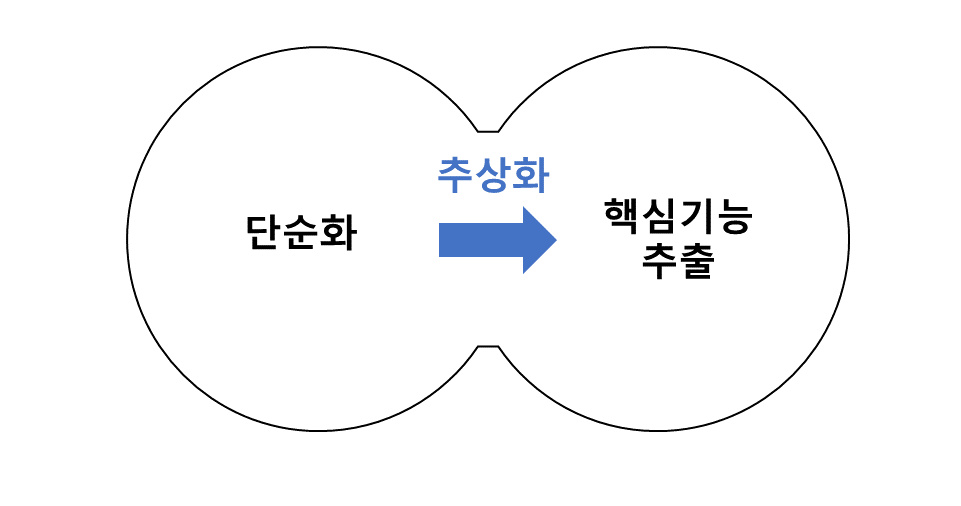
■ 추상화 (Abstraction) 과정의 필요
- 실제 세계의 문제는 매우 복잡함 ( 즉 실제 Arad에서 Bucharest까지 가능 방식은 매우 다양함 )
- 인공지능에서 문제를 풀기 위해서는 단순화 과정이 필요함
- Romania 예제에서는 "Arad라는 도시에 있는 상황을 1개의 state로, action을 통해 Zerind라는 state로 간다"
(e.g Arad → Zerind)라는 사실을 추상화해서 표현
- 따라서 해(solution) 자체도 단순화된 추상화 형태로 표현 ( 즉 인공지능이 해결 가능한 형태로 표현 )
+ 컴퓨터 사고력에서의 추상화 (abstraction)
- 문제를 단순화시켜 불필요한 부분은 제거하고 핵심 요소와 개념 또는 기능을 간추려 일반화된 모델(Generalized model)을 만드는 과정
memo : 문제 해결하는데 실제 지도 구현은 힘듦. => 우리가 풀고자 하는 문제로만 봄 (ex: 고속도로)
■ 8-Puzzle 문제 (Problem Formulation)

- 상태 (state) : Location of tiles : 8개의 타일의 각각의 위치와 빈칸의 위치
- 동작 (action) : Move blank Left, Right, Up, Down : 빈칸으로 왼쪽, 오른쪽, 위, 아래 이동
- 목표 도달 확인 (Goal test) : 주어진 목표상태에 도달했는지 확인
- 경로 비용 (Path cost) : 한번 action할 때마다 1씩 증가 (경로의 수)
3. 탐색 전략 (Search Strategy)
상태공간 그래프 (State Space Graph)
- 인공지능에서는 상태공간에서 최적의 해 (Optimal solution)를 찾기 위해, 각 동작 (Action)에 따른 상태 변화를 그래프로 나타내어 해결 함
■ 8-Puzzle 문제 (Problem Formulation)

■ Romania Example에 대한 Tree Graph 표현
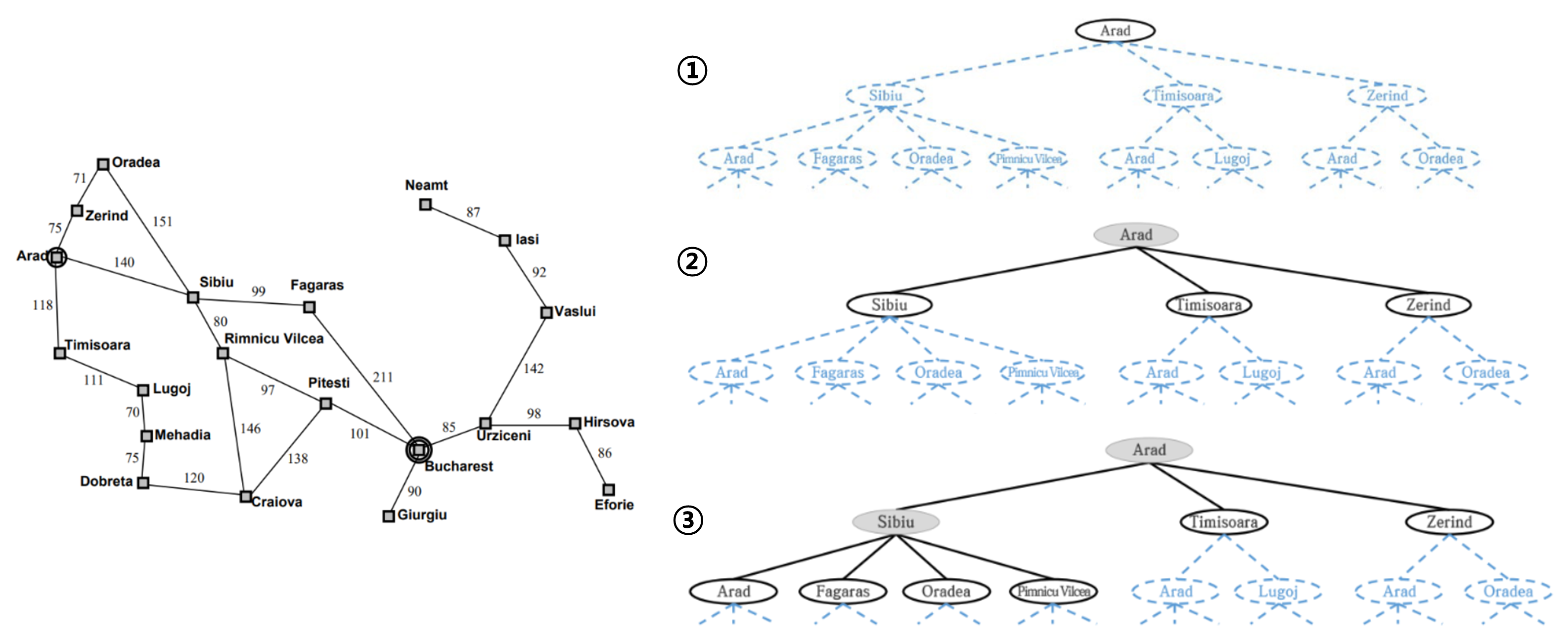
■ Tree 구조로 상태 공간 (State Space) 표현
- Root 노드 : 초기 상태 (Initial State)
- 각 Node는 상태 (State)를 나타냄
- 동작 (Action)은 Tree에서 가지 (Branch), Child Node는 갈 수 있는 Next State를 의미함
탐색은 잠재적인 다음 상태 (Possible next state)로 움직이고, 또다시 어느 상태 (state)로 움직일지 결정해서 다음과정으로 가는 것을 반복하여 Goal State를 찾는 과정
탐색 전략 (Search Strategy)
- Tree 구조에서 어떠한 순서로 노드를 확장할지(i.e., 어느 상태(state)로 움직일지) 고르는 전략
■ 탐색 전략 선택의 4가지 기준
- Completeness (완전성) : 해(solution)가 있다면 반드시 찾을 수 있는가?
- Time Complexity (시간 복잡도) : 얼마만큼 노드를 확장해야 목표상태에 도달 할 수 있는가?
- Space Complexity (공간 복잡도) : 메모리 공간에 저장할 수 있는 최대 노드의 개수는 몇 개인가?
- Optimality (최적성) : 가장 적은 비용이 드는 최적의 해(solution)를 찾을 수 있는가?
memo : 다 만족하는 알고리즘은 없음
탐색전략 4가지는 각각 Trade-off (상충관계)가 있음 - 즉 한쪽 전략은 좋지만 다른 한쪽은 안좋음
→ 문제에 따라 적절한 전략 선택이 중요함
■ 탐색 전략 종류
- 무정보 탐색 (Uninformed Search, Blind Search) - 맹목적 탐색
- 정보이용 탐색 (Informed Search)
- 지역 탐색 (Local Search)
- 게임 탐색 (Game Search)

4. 무정보 탐색 (Uninformed Search)
■ 무정보 탐색이란?
- 주어진 정보만을 활용해서 탐색을 하는 방법
- 즉 상태공간에 대한 아무런 정보 없이, 정해진 순서에 따라 상태 공간 그래프를 점차 생성해 가면서 해를 탐색하는 방법
- 대표 방법 (6가지)
- 너비우선 탐색 (Breadth-First Search)
- 균일비용 탐색 (Uniform-Cost Search)
- 깊이우선 탐색 (Depth-First Search)
- 깊이제한 탐색 (Depth-Limited Search)
- 반복적 깊이 심화 탐색 (Iterative Deepening Search)
- 양방향 탐색 (Bidirectional Search)
01. 너비우선탐색 (Breadth-First Search)
- 초기 노드에서 시작하여 모든 자식 노드를 확장하여 생성
- 아직 펼쳐지지 않은 노드(fringe)가 있다면 가장 얕은 노드(shallow node)부터 펼쳐보는 방법
- BFS는 FIFO(First-In-First-Out) queue를 이용함
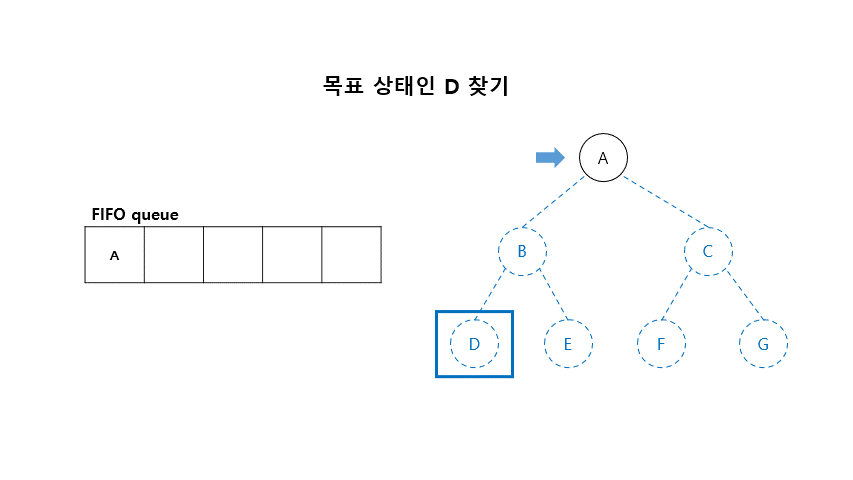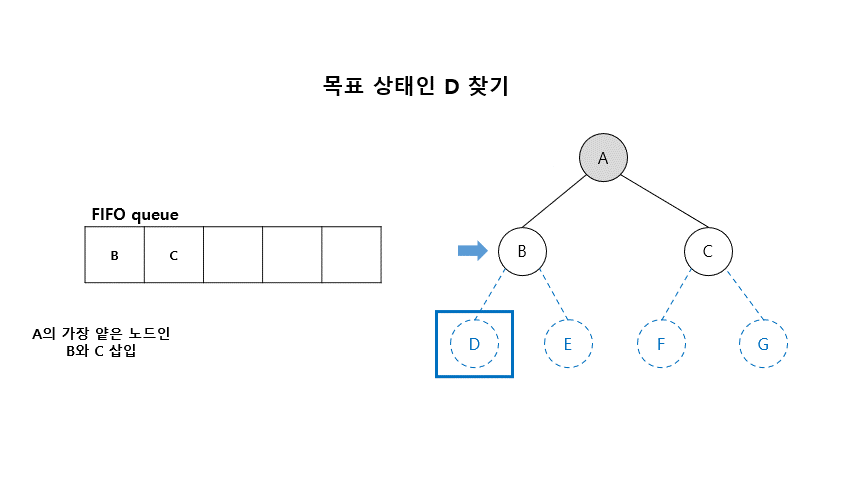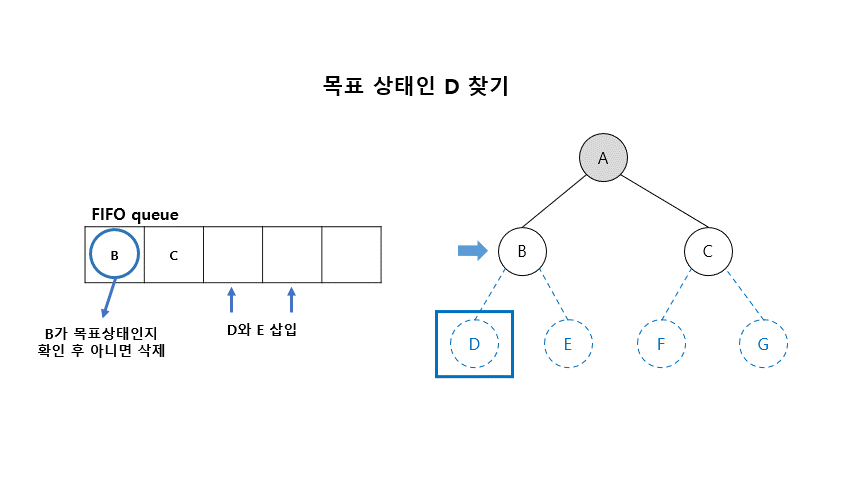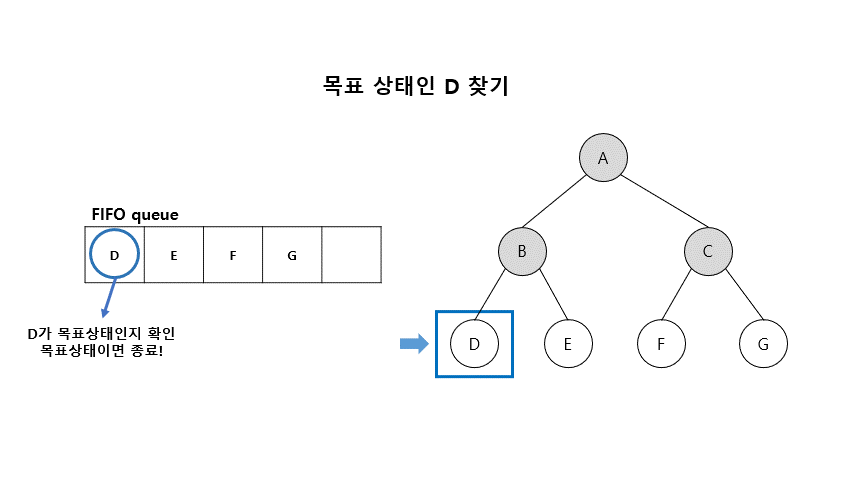
■ 너비 우선 탐색 알고리즘
- Open (리스트) : 확장은 되었으나 아직 탐색하지 않은 상태들의 들어 있는 리스트
- Closed (리스트) : 탐색이 끝난 상태들이 들어 있는 리스트
Breadth_First_Search()
open <- [시작노드]
closed <- []
while open ≠ [] do
X <- open 리스트의 첫 번째 요소
if X == goal then return SUCCESS
else
X의 자식 노드를 생성함
X를 closed 리스트에 추가함
X의 자식 노드가 이미 open이나 closed에 있다면 버림
남은 자식 노드들은 open의 끝에 추가함 ( 큐처럼 이용 )
return FAIL
02. 깊이우선탐색 (Depth-First Search)
- 초기 노드에서 시작하여 깊이 방향으로 탐색
- 가장 깊은 아직 펼쳐지지 않은 노드(fringe)들 부터 하나씩 체크하고 펼쳐보는 방법
- DFS는 LIFO (Last-In-First-Out) queue 방법을 이용함 (Stack)
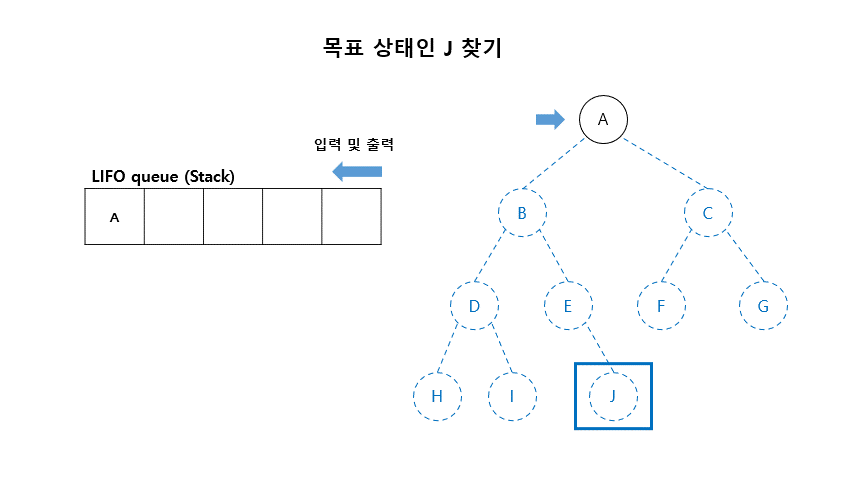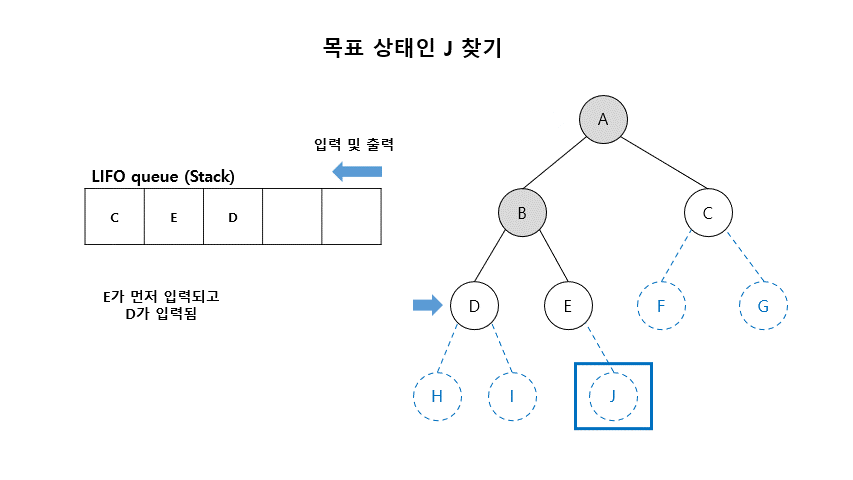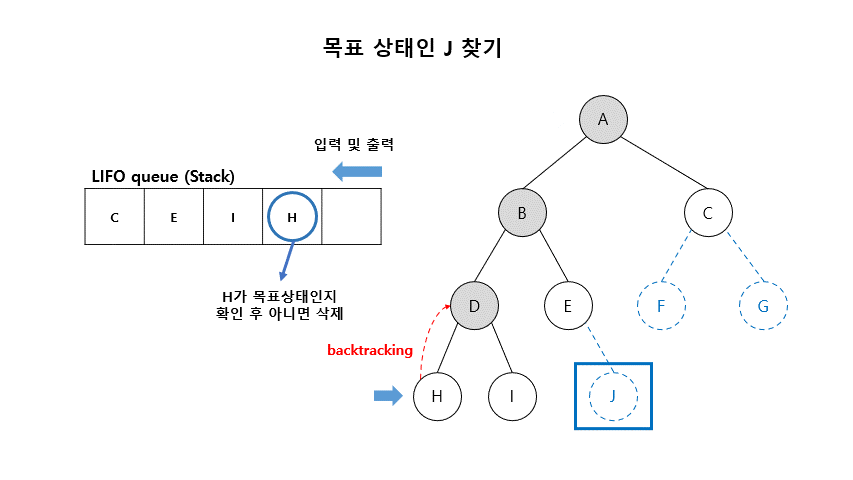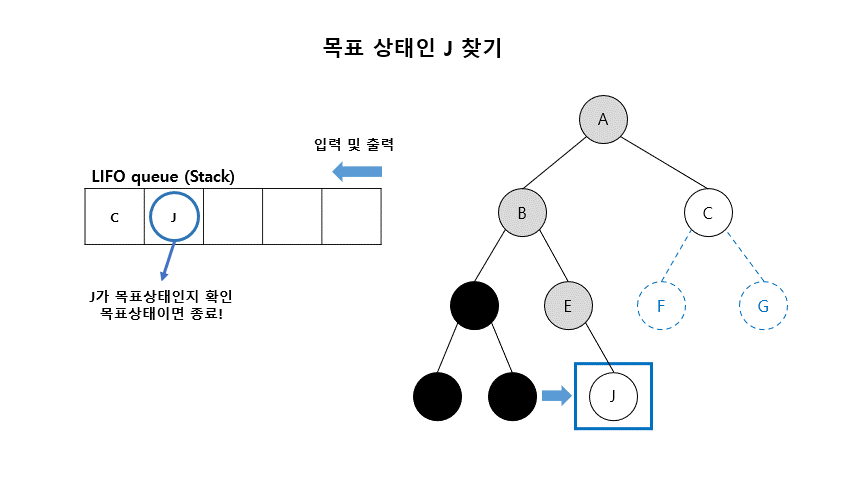
■ 깊이 우선 탐색 알고리즘
- Open (리스트) : 확장은 되었으나 아직 탐색하지 않은 상태들이 들어 있는 리스트
- Closed (리스트) : 탐색이 끝난 상태들이 들어 있는 리스트
Depth_First_Search()
open <- [시작노드]
closed <- []
while open ≠ [] do
X <- open 리스트의 첫 번째 요소
if X == goal then return SUCCESS
else
X의 자식 노드를 생성함
X를 closed 리스트에 추가함
X의 자식 노드가 이미 open이나 closed에 있다면 버림
남은 자식 노드들은 open의 처음에 추가함 ( 스택처럼 이용 )
return FAIL
BFS vs. DFS
■ 너비 우선 탐색 및 깊이 우선 탐색 비교
- b (branch num) : 한 노드에서 펼쳐질 수 있는 최대의 숫자
- d (goal depth) : 목표 상태가 있는 depth(깊이)
- m (search depth) : 검색하게 될 depth(깊이)
| BFS | DFS | |
| Complete? | Yes | No |
| Time | O(bᵈ⁺¹) | O(bᵐ) |
| Space | O(bᵈ⁺¹) | O(bm) |
| Optimal? | Yes | No |
- 완전성 : BFS는 만족, DFS는 불만족 (무한루프에 빠지거나 아주 깊은 깊이로 메모리 초과 가능)
→ DFS의 경우 완전성 만족을 위해 unbounded depth (깊이 제한)을 두어 탐색하기도 함
- 시간 복잡도 : BFS는 DFS보다 복잡도가 큼 (목표상태가 있는 깊이데 따라 시간이 걸림)
- 공간 복잡도 : BFS는 DFS보다 메모리 공간을 더 많이 필요
- 최적성 : BFS 만족, DFS 불만족 ( DFS는 완전성이 불만족이므로 최적의 해 못 찾을 수 있음)
■ 너비 우선 탐색 및 깊이 우선 탐색 비교 (어느 쪽이 좋을까?)
- BFS와 DFS 중 어떤 게 더 좋다고 말할 수는 없음 (문제에 따라 다름)
- 시간, 공간복잡도로 인해 상태공간그래프가 크다면 DFS 고려
- 검색대상 규모가 크지 않고, 초기상태로 부터 목표상태까지 멀지 않다면 BFS
- DFS로 경로를 검색한다고 할 때, 처음 발견되는 해(solution)이 최단 거리는 아닐 수 있음
- 반대로 BFS로 경로를 검색한다고 할 때, 처음 발견되는 해(solution)는 최단 거리임
03. 균일비용탐색 (Uniform Cost Search)
- 최소 경로비용을 기준으로 한 BFS의 일반화 버전 = Dijkstra Algorithm
- 가장 깊은 아직 펼쳐지지 않은 노드(fringe)들마다 비용을 적어 가장 적은 비용으로 탐색
- FIFO (First-In-First-Out) queue를 이용
- Uninformed Search에서 BFS, DFS는 임의 경로 탐색이지만, UCS는 최적경로 탐색 기법
- Path cost라는 정보를 활용하는 것 같지만, 과거부터 현재 노드만 사용되며 Target 노드에 대한 정보는 활용되지 않음
- 균일비용탐색(무정보) - 출발노드로부터 현재노드까지 거리
- 최상우선탐색(정보) - 현재노드로부터 목표노드까지의 거리 (휴리스틱)
- A* 알고리즘(정보) - 출발노드로부터 현재노드까지 거리 + 현재노드로부터 목표노드까지 거리 (휴리스틱)

- 시작 노드부터 goal인지 검사한 후, 노드를 확장하고 비용이 작은 fringe 선택함
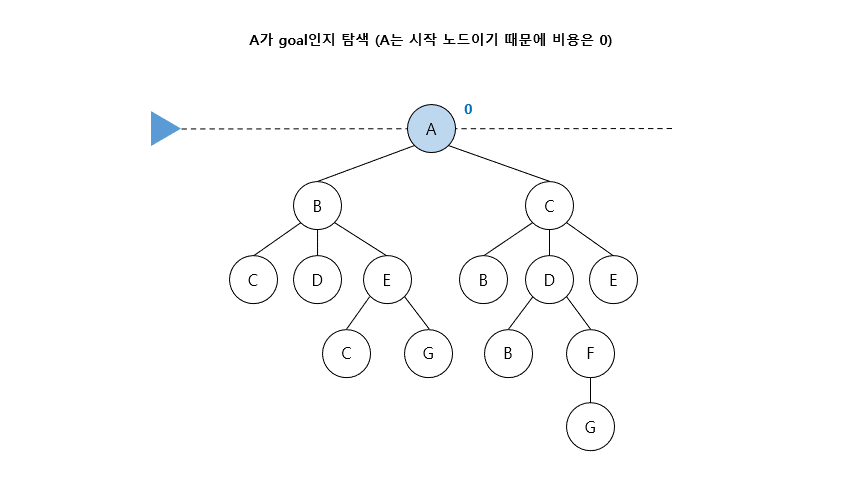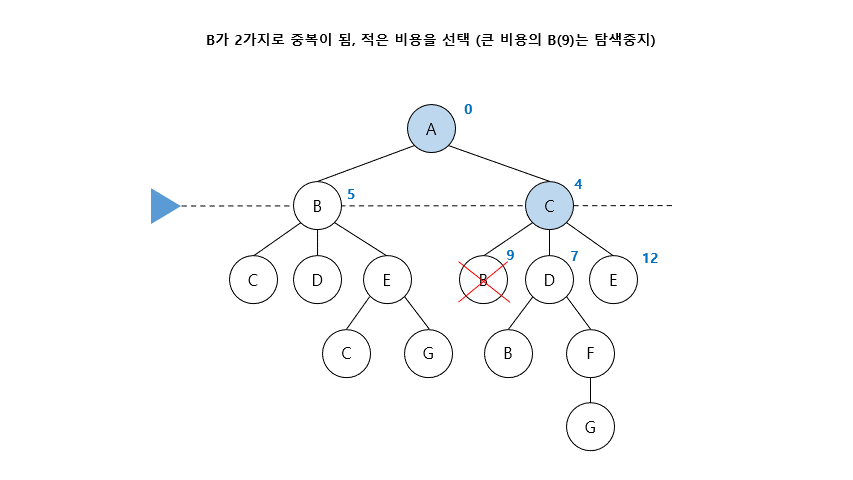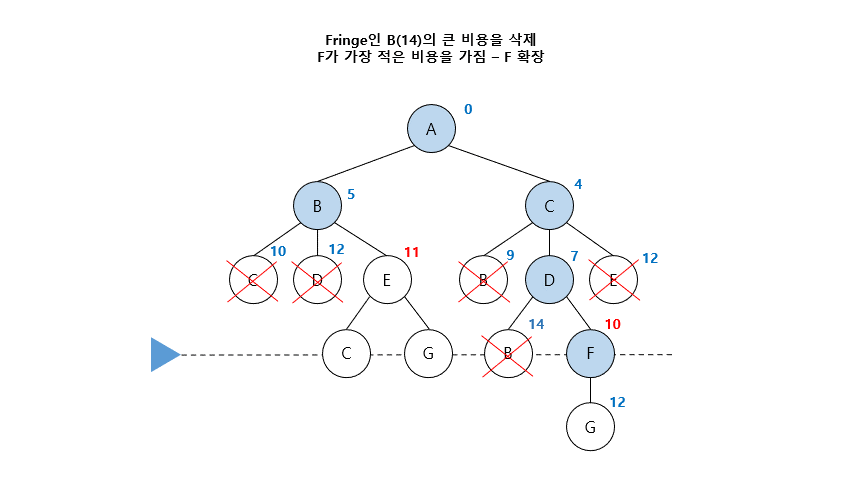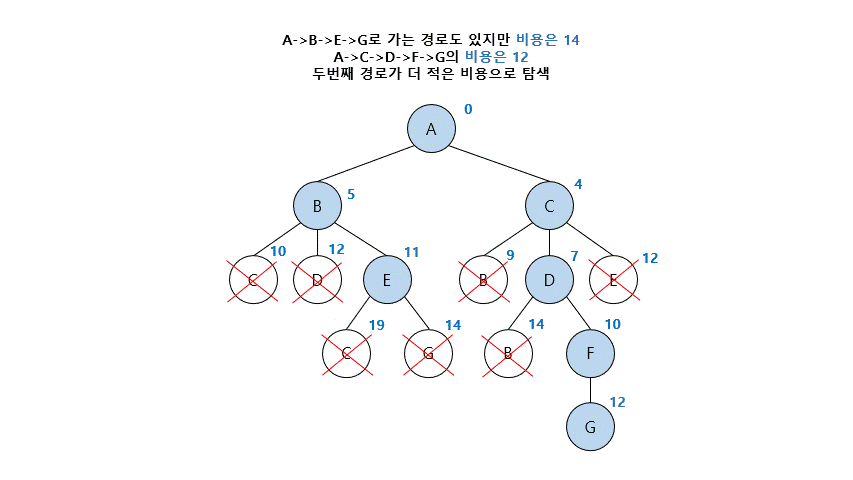
- 노드가 중복이 된다면, 적은 비용을 선택함 ( 큰비용의 노드는 탐색 중지)
- 마지막으로 노드를 확장하게 된다면, 확장할 값이 없기 때문에 그 노드가 Goal임
04. 반복적깊이심화탐색 (Iterative Deepening Search)
- DFS의 경우 메모리 부담은 적으나 최단 경로를 찾는다는 보장이 없으며, BFS의 경우 반대로 메모리 부담은 많으나 최단경로를 찾는 것을 보장함
→ DFS와 BFS의 장점을 합친 방법은 없을까? IDS (반복적 깊이심화탐색)
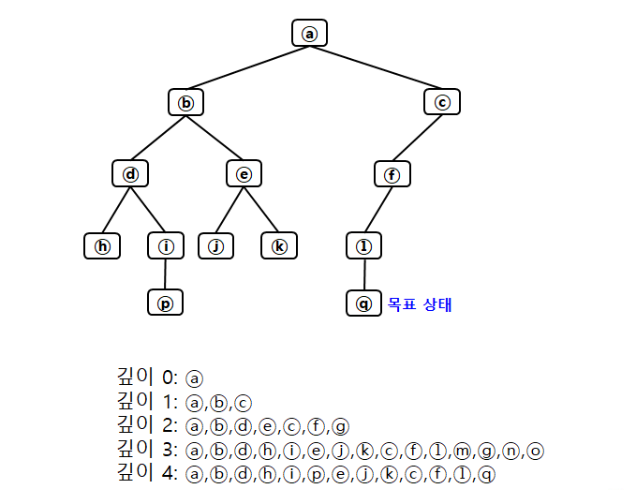
■ IDS (반복적 깊이심화탐색)
- 깊이 한계(Depth Limit)을 0에서 점차 1씩 증가시켜가면서 DFS로 탐색하는 방법
- 최단 경로 해 보장
- 메모리 공간 사용 효율적 (기본적으로는 DFS를 따르기 때문)
- 반복적인 깊이 우선 탐색에 따른 비효율성 (즉 깊이가 늘어날때마다 DFS를 수행해야함)
- 실제 비용이 크게 늘지 않음
- 각 노드가 10개의 자식노드를 가질 때, 너비 우선 탐색 대비 약 11%정도 추가 노드 생성
05. 양방향탐색 (Bidirectional Search)
- BFS의 경우 탐색 범위가 넓어지면 상태공간그래프에 생성해야하는 노드의 개수가 크게 증가할 수 있음
- 이러한 문제를 해결하기 위해 초기상태와 목표상태를 기준으로 번갈아 가면서 BFS를 진행하는 양방향 탐색 수행
( 중간지점에서 만나도록하여 최적의 해를 찾는 방법 )
- BFS의 장점을 취하면서, 적은 노드의 수만 사용하여 시간 및 공간복잡도가 BFS보다 우수

'학교 공부 > 인공지능' 카테고리의 다른 글
| [23-01/인공지능] 지식표현과 추론 - 2 (2) | 2023.04.26 |
|---|---|
| [23-01/인공지능] 지식표현과 추론 - 1 (3) | 2023.04.26 |
| [23-01/인공지능] 문제해결 및 탐색전략 - 2 (2) | 2023.04.25 |
| [23-01/인공지능] 인공지능의 발전과정, 지능형 에이전트 (2) | 2023.04.17 |
| [23-01/인공지능] 인공지능 개요 (1) | 2023.04.17 |



