- C
- datastructure
- programmers
- codingTest
- Baekjoon
- Personal_Study
- Image_classification
- 2023_1st_Semester
- Algorithm
- Operating_System
- Kubernetes
- Android
- 리눅스마스터2급
- SingleProject
- 티스토리챌린지
- kubeflow
- app
- Univ._Study
- Artificial_Intelligence
- 자격증
- Python
- Database_Design
- Linux
- study
- 오블완
- Unix_System
- Java
- c++
- tensorflow
- cloud_computing
코딩 기록 저장소
[23-01/인공지능] 문제해결 및 탐색전략 - 2 본문
탐색 전략
■ 탐색 전략 (Search Strategy) 종류
- 무정보 탐색 (Uninformed Search, Blind Search (맹목적 탐색) )
- 정보 이용 탐색 (Informed Search)
- 지역 탐색 (Local Search)
- 게임 탐색 (Game search)

1. 정보이용 탐색 (Informed Search)
■ 정보이용 탐색이란?
- 상태 공간에 대한 추가적인 정보나 지식을 활용해서 탐색 하는 방법
- 정보이용 탐색은 휴리스틱(H(n), 평가함수)을 활용하기 때문에 휴리스틱 탐색(Heuristic Search)이라고도 함
- 휴리스틱(Heuristic) : 최적의 해를 찾다는 보장(Optimality)은 없지만, 신속한 어림짐작을 통해 충분히 좋은 해를 찾을 수 있는 경험적 지식
memo : 휴리스틱 함수 - 두가지의 길이 있을 때 이 중 어떤게 빠른 길일까 평가해서 이 길을 택하겠다. 하는 함수

memo : 두 탐색 비교하는 그림. Uninformed는 정보가 없기 때문에 모든 것들을 탐색해나가면서 Goal까지 도착함. 하지만 Informed는 Goal까지 가는데 정보가 주어져서 다 탐색하지 않고 효율적인것만 택하여 Goal까지 도달 가능 함
■ 대표방법 (4가지)
- 최선우선탐색 (Best-First Search)
- 빔 탐색 (Beam Search)
- A* 알고리즘 (A* Algorithm)
- 언덕오르기 알고리즘 (Hill-Climbing Algorithm)
memo : Local Search도 정보 이용 탐색의 한 부분.
■ 휴리스틱( H(n), 평가함수)을 통한 추정의 예
- 맹목적 탐색은 정해진 룰을 따라 탐색(e.g. 가장 얕은 노드부터/깊은 노드부터 펼침)을 하지만 정보이용함수는 휴리스틱(평가함수)를 참고하여 탐색 진행

● 최단 경로 문제
- (휴리스틱) 현재 위치에서 목적지까지 직선 거리
● 8-퍼즐 문제
- (휴리스틱) 제자리에 있지 않은 타일의 개수
01. 최선 우선 탐색 (Best-First Search)
최선 우선 탐색
- 확장 중인 노드들 중에서 목표 노드까지 남은거리가 가장 짧은 노드를 확장하여 탐색하는 방법
- 휴리스틱(평가함수) : f(n) = h(n) (heuristic)
memo : Greedy Search라고도 함. 가장 좋은 것만 택함. 그리디도 마찬가지임. 탐욕적으로 제일 좋은걸 택함.
■ 최단 경로 문제


memo : 현재 상황에서 가장 좋은 것. 가장 가까운 것을 택함. 확장 중인 노드 중에서 목표 노드까지 남은 거리가 가장 짧은 노드. 가장 좋은 노드만 확장해서 탐색해나가는 방법.
■ 8-Puzzle에서의 Best-First Search 예제
- 휴리스틱(평가함수) : 제자리가 아닌 타일의 개수

memo : 어차피 알고즘이므로 정해진 방법대로 순차적으로 탐색함. 만약 랜덤으로 한다면 랜덤으로 탐색하게됨.
최선우선탐색 알고리즘
- open 리스트 : 확장은 되었으나 아직 탐색하지 않은 상태들이 들어 있는 리스트
- closed 리스트 : 탐색이 끝난 상태들이 들어 있는 리스트
Best_First_Search()
open < [시작노드]
closed < []
while open ≠ [] do
X < open 리스트의 첫 번째 요소
if X == goal then return SUCCESS
else
X의 자식 노드를 생성함
X를 closed 리스트에 추가함
if X의 자식 노드가 open이나 closed에 있지 않으면
자식 노드의 휴리스틱(평가함수) 값을 계산함
자식 노드들을 open에 추가함
return FAIL
memo : 이 BFS는 찾긴 찾음. 이것은 유한하면 이 탐색은 성공할 수 있음. 근데 굉장히 큰 데이터. 무한해진다면 못찾을 수도 있음.
02. A* 알고리즘
A-Star 알고리즘 (A* Algorithm)
- 추정한 휴리스틱(평가함수) f(n)의 값이 최소인 노드를 확장해 가는 방법
f(n) = g(n) + h(n)
- g(n) : 시작 노드에서 현재 노드 n까지의 비용 <- 이부분이 추가됨
- h(n) : 현재 노드 n에서 목표 노드(goal)까지의 비용
- f(n) : 노드 n을 경유하여 목표 노드(goal)까지 도달 하는데 드는 전체 비용
→ 즉 A* 알고리즘은 h(n)을 통해 현재 노드에서 goal까지 도달하는데 가장 빠른 노드를 펼치지만, g(n)을 통해 노드까지 가는데 이미 비싼 비용을 치렀다면, 그 노드를 더 이상 펼치지 말고 비용이 더 적은 노드를 중점적으로 활용하는 알고리즘
memo : 네비게이션에 많이 씀. 어디까지 가려고 할때 GPS기반으로 찾아가는 알고리즘
■ 최단 경로 문제

■ 8-Puzzle

A-Star 알고리즘 (A*Algorithm)
Astar_Search()
open < [시작노드]
closed < []
while open ≠ [] do
X < open 리스트의 첫 번째 요소
if X == goal then return SUCCESS
else
X의 자식 노드를 생성함
X를 closed 리스트에 추가함
if X의 자식 노드가 open이나 closed에 있지 않으면
자식 노드의 휴리스틱(평가함수) : f(n) = g(n) + h(n) 값을 계산함
자식 노드들을 open에 추가함
return FAIL
Admissible Heuristic (허용가능한 휴리스틱) ★
■ A* 알고리즘은 최적의 해(Optimality)를 보장하는가?
- 경험적탐색에서는 사용되는 휴리스틱 함수에 큰 영향을 받음
- 즉 휴리스틱 함수가 얼마나 좋은지에 따라 알고리즘의 성능을 결정함 (개발자의 선택)
-> 따라서 개발자의 선택에 의해 활용되는 휴리스틱 함수는 언제나 최적의 해를 보장하지 못함
■ Admissble Heuristic
- 만약 휴리스틱 함수 값이 현재 node에서 goal까지의 실제 cost보다 항상 작거나 같은 경우에는 최적의 해를 보장하며 이를 허용가능이라 함. h(n) <= h*(n)
■ Admissble Heuristic (허용가능한 휴리스틱)
- 만약 휴리스틱 함수 값이 node에서 goal까지의 실제 cost보다 길다면? h(n) > cost

A* 알고리즘은 상황에 따라 Optimal하거나 Optimal하지 않음
-> 휴리스틱 값이 Cost 값보다 높을 때(h(n)>cost) Optimal 하지 않음
반드시 Cost 값보다 h(n)이 작거나 같아야 Optimal함 (Admissible)
A * Algorithm의 최적성 (Optimality)
- Proof (Cost값보다 h(n)이 작거나 같으면 Optimal 할까?)

Best-First Search vs. A* Algorithm
■ 최선우선탐색 vs. A*알고리즘 비교
- b (branch num) : 한 노드에서 펼쳐질 수 있는 최대의 숫자
- d (goal depth) : 목표 상태가 있는 depth(깊이)
- m (search depth) : 검색하게 될 depth(깊이)
| Criterion | Best-First Search | A* Algorithm |
| Complete? | No | Yes (단 admissble한 경우) |
| Time | O(bᵐ) | O(bm) |
| Space | O(bᵐ) | O(bᵐ) |
| Optimal | No | Yes (단 admissble한 경우) |
- 완전성 : 최선우선탐색 불만족, A*는 만족
- 시간복잡도 : 휴리스틱 알고리즘에 따라 차이가 있으나 A*가 빠름
- 공간복잡도 : 최선우선탐색, A* 동일
- 최적성 : 최선우선탐색 불만족, A*는 만족
2. 지역 탐색 (Local Search)
지역탐색
■ 지역탐색 (Local Search)
- 탐색 관련 문제에서는 Goal까지 어떻게 도달하는지에 대한 Path보다 Goal을 달성하는지 자체가 더 중요할 때가 많음
- Global(전역적)으로 모든 Path를 고려하여 Goal에 도달하는 것보다, 주변 상태만을 보고 즉 Local(지역적)으로 탐색하여 Goal에 도달
- 이러한 경우, 지역 탐색 (Local Search) 사용
- 현재노드를 기준으로 이웃 노드들을 확인하여 조금이라도 더 좋은 노드로 이동하는 방식
memo : 사실 요즘 탐색 방법은 state 상태를 전부 알아야 구현 가능한 알고리즘. 근데 이건 데이터가 너무 많음 딥러닝 머신러닝 데이터 많으면 state를 다 정의 못할 때가 있음. 기존의 알고리즘을 못쓰나? 그렇진 않음. 이것을 다르게 보자!
● 2가지 장점 발생
1. 작은량의 메모리 사용 : 현재상태만 기억하고 있으므로, 사용되는 메모리가 작음
2. 매우 크거나 무한한 상태공간에 대한 합리적인 해 도출 가능 (전역적인 경우 많은 시간 필요)
memo : 무한한 상태 Goal을 도달하는 솔루션 -> 이것은 Optimal, Complete할까? 찾을 수 있는 경우도 있고 아닌 경우도 있음. 아무것도 안보이는 미로에서 Goal을 찾아갈 때 찾아가는 것은 자기의 감. 그것만 이용해서 가면 Goal까지 잘 도착할 수도 있고, 아닐수도 있음. 그런 알고리즘임. 하지만 문제를 좁혀주면 찾아갈 수 있음.
■ 지역탐색 (Local Search) 예제
● N-Queens
- 체스에서 여왕(Queen)은 가로, 세로, 대각선 어디로든 움직일 수 있음
- 이러한 여왕이 N × N 보드 위에 N개 있다고 가정할 경우, 여왕이 서로 공격하지 상태를 만드는 것이 목표

01. 언덕오르기 알고리즘
언덕오르기 알고리즘 (Hill-Climbing Algorithm)
- 현재의 노드에서 휴리스틱에 의한 평가값이 가장 좋은 이웃 노드 하나를 확장해 가는 탐색 방법
- 즉 최적의 해를 찾아 값이 증가하는 방향이나 감소하는 방향으로 계속 이동하는 알고리즘
- 언덕오르기 알고리즘 moto : 언덕을 올라가는 과정을 모사하여 만들어진 알고리즘으로, 짙은 안개속에 에베레스트 산을 등반할 때 주변에서 가장 경사가 높은 곳으로 올라가면 산 정상에 올라갈것이다라고 가정

memo : 단점. 예를 들어 A가 언덕을 오르게 되면 A와 가까운 꼭대기에 올라가 멈추게 되면 A 입장에서는 여기가 베스트 솔루션이 됨. 하지만 전체 문제로 봤을 땐 B쪽의 언덕이 베스트 솔루션임 - 시작이 어디냐에 따라서 문제를 풀수 있는 솔루션으로 갈 수 있느냐 없느냐라는 문제가 생김. 초기 상태에 따라 결괏값이 달라질 수 있음
■ 8-Queens problem
- 각 상태는 열마다 하나씩 8개의 queen을 가짐
- 각 queen을 동일 열 내 다른 위치로 이동시킴으로써 총 56개의 successor(후속상태) 상태 생성
- h는 서로 공격 가능한 쌍의 수
- 숫자는 그 열의 Queen을 옮겼을 때 공격가능 수

- 임의의 시작점으로부터 과정을 계속 반복하여 Queen을 옮길 경우, h = 1인 상황에 도달
- 즉 Hill-Climbing 방법은 최적의 해를 구할 수 없을 수도 있음 -> Local Maximum에 빠짐

■ 언덕 오르기 알고리즘 단점
- 시작상태(Initial State)에 따라, Local Maximum에 빠질 수 있음
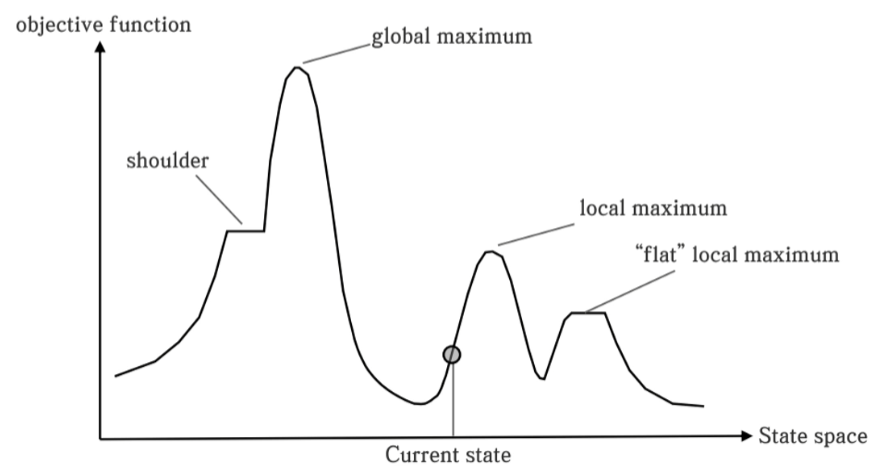
memo : 이 알고리즘은 결국에 기울기만 봄. 기울기가 증가하면 쫓아가지만 감소하면 더이상 안봄.
이걸 푸는 문제 크게 2가지. 하나의 솔루션은 Current State를 랜덤하게 몇개 만듦. 그리고 여러번 반복하여 결과를 얻음. - Iteration
02. Simulated Annealing Search
■ Simulated Annealing Search
- Hill-Climbing 알고리즘을 기반으로 함
- 기존의 Hill-Climbing 알고리즘은 꼭대기에 도착하고 기울기가 감소되면 더이상 안보지만 이 알고리즘은 떨어지더라도 일정부분 가봄.
- '언덕오르기 알고리즘' 보완을 위해 만들어짐
3. 게임 탐색 (Game Search)
■ Tic - Tac - Toe 게임
- 2인용 게임
- 두 경기자를 MAX와 MIN으로 부름
- 항상 MAX가 먼저 수를 둔다고 가정함

● Tic - Tac - Toe 게임 트리
- 상대가 있는 게임에서 자신과 상대방의 가능한 게임 상태를 나타낸 트리 (틱택톡, 바둑, 장기, 체스 등)
- 게임의 결과는 마지막에 결정
- 많은 수(Lookahead)를 볼 수록 유리

01. Min-Max 알고리즘
Min-Max 알고리즘 (mini-max algorithm)
- MAX 노드 : 자신에 해당하는 노드로 자기에게 유리한 최대값 선택
- MIN 노드 : 상대방에 해당하는 노드로 최소값 선택
- 단말 노드부터 위로 올라가면서 최소 (minimum) - 최대 (maximum) 연산을 반복하여 자신이 선택할 수 있는 방법 중 가장 좋은 것은 값을 결정

● Min-Max 알고리즘
- 부모 노드에서는 노드 자체에서 점수를 계산하지 않고 자식 노드에서 평가되고 결정된 점수를 부모 노드에 올려 주면 됨.

● 시간복잡도
- 미니맥스 알고리즘은 게임 트리에 대하여 완벽한 깊이 우선 탐색을 수행
- 만약 트리의 최대 깊이가 m이고 각 노드에서의 가능한 수가 b개라면 최대최소 알고리즘의 시간 복잡도는 O(bᵐ)임
-> 바둑은 경우의 수가 약 316!임. 이것을 계산해보면 약 10⁷⁶¹ 로 추산됨
02. Alpha-Beta 알고리즘
Alpha-Beta 알고리즘 (α-β algorithm)
■ 아이디어
- Min-Max 알고리즘은 탐색 공간 전체를 탐색하는 것을 가정함
- 하지만 실제로는 탐색 공간의 크기가 무척 크기 때문에 단점이 발생
- Min-Max 알고리즘에서 형성되는 탐색 트리 중 상당 부분은 결과에 영향을 주지 않기 때문에 가지들을 쳐낼 수 있음
-> 이를 Alpha-Beta 알고리즘 (가지치기, pruning)이라고 함
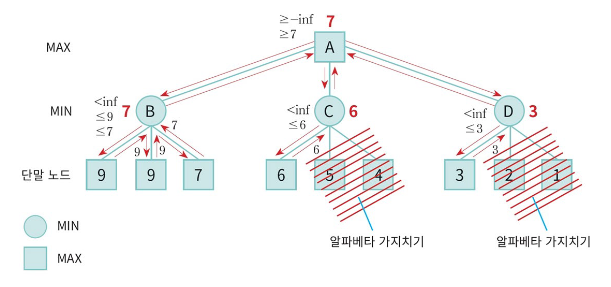
■ Alpha-Beta 알고리즘
- 검토해 볼 필요가 없는 부분을 탐색하지 않도록 하는 기법
- 깊이 우선 탐색(DFS)으로 제한 깊이까지 탐색을 하면서, MAX 노드와 MIN 노드의 값 결정
- α-자르기(cut-off) : MIN 노드의 현재값이 부모노드의 현재 값보다 작거나 같으면, 나머지 자식 노드 탐색 중지
- β-자르기 : MAX 노드의 현재값이 부모노드의 현재 값보다 같거나 크면, 나머지 자식 노드 탐색 중지

'학교 공부 > 인공지능' 카테고리의 다른 글
| [23-01/인공지능] 지식표현과 추론 - 2 (2) | 2023.04.26 |
|---|---|
| [23-01/인공지능] 지식표현과 추론 - 1 (3) | 2023.04.26 |
| [23-01/인공지능] 문제해결 및 탐색전략 - 1 (0) | 2023.04.19 |
| [23-01/인공지능] 인공지능의 발전과정, 지능형 에이전트 (2) | 2023.04.17 |
| [23-01/인공지능] 인공지능 개요 (1) | 2023.04.17 |




