- Personal_Study
- Artificial_Intelligence
- Image_classification
- tensorflow
- Android
- Linux
- Baekjoon
- Operating_System
- kubeflow
- 리눅스마스터2급
- cloud_computing
- 오블완
- 티스토리챌린지
- Java
- Python
- Algorithm
- codingTest
- Unix_System
- C
- app
- 자격증
- c++
- 2023_1st_Semester
- Univ._Study
- datastructure
- study
- Database_Design
- Kubernetes
- SingleProject
- programmers
코딩 기록 저장소
[알고리즘] 정렬 본문
1. 기본적인 정렬 알고리즘
선택 정렬
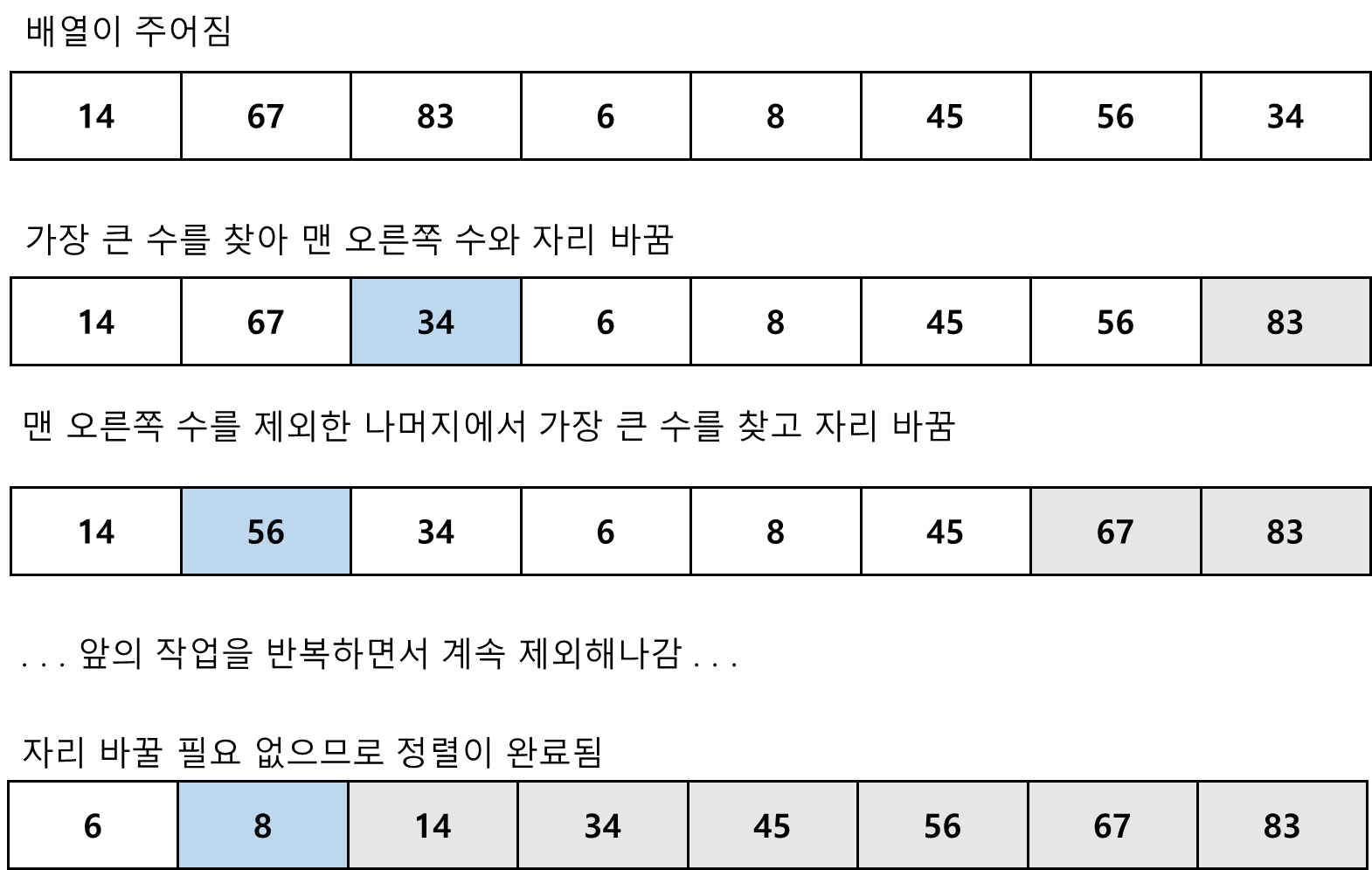
- 선택 정렬은 원리가 간단한 정렬 알고리즘 중 하나.
- 배열 A[1~n]에서 가장 큰 원소를 찾아 이 원소와 배열의 끝자리에 있는 A[n]과 자리를 바꿈.
- 맨 뒷자리로 옮긴 가장 큰 원소는 제외하고 나머지 원소들로 같은 작업을 반복함.
selectionSort(A[],n)
{
① for last <- n downto 2 {
② A[1 ~ last] 중 가장 큰 수 A[k]를 찾음;
③ A[k] <->A[last]; // A[k]와 A[last]의 값을 교환함
}
}
①에서 변수 last는 정렬할 배열의 맨 마지막 인덱스, 즉 배열의 크기를 나타냄. 처음에는 배열의 크기가 n으로 시작하므로 A[1 ~ n]을 정렬 대상으로 삼음. 가장 큰 수를 찾아 제자리에 놓을 때마다 last는 1씩 줄어듦.
- for 루프는 정렬할 배열의 크기를 한 번에 하나씩 줄여나가는 역할을 함.
- 계속 작아지다가 마지막에는 크기 2인 배열의 원소중 큰 원소를 A[2]에 놓고나면 A[1]에는 제일 작은 원소가 자리잡게 되므로 정렬이 끝남.
버블 정렬
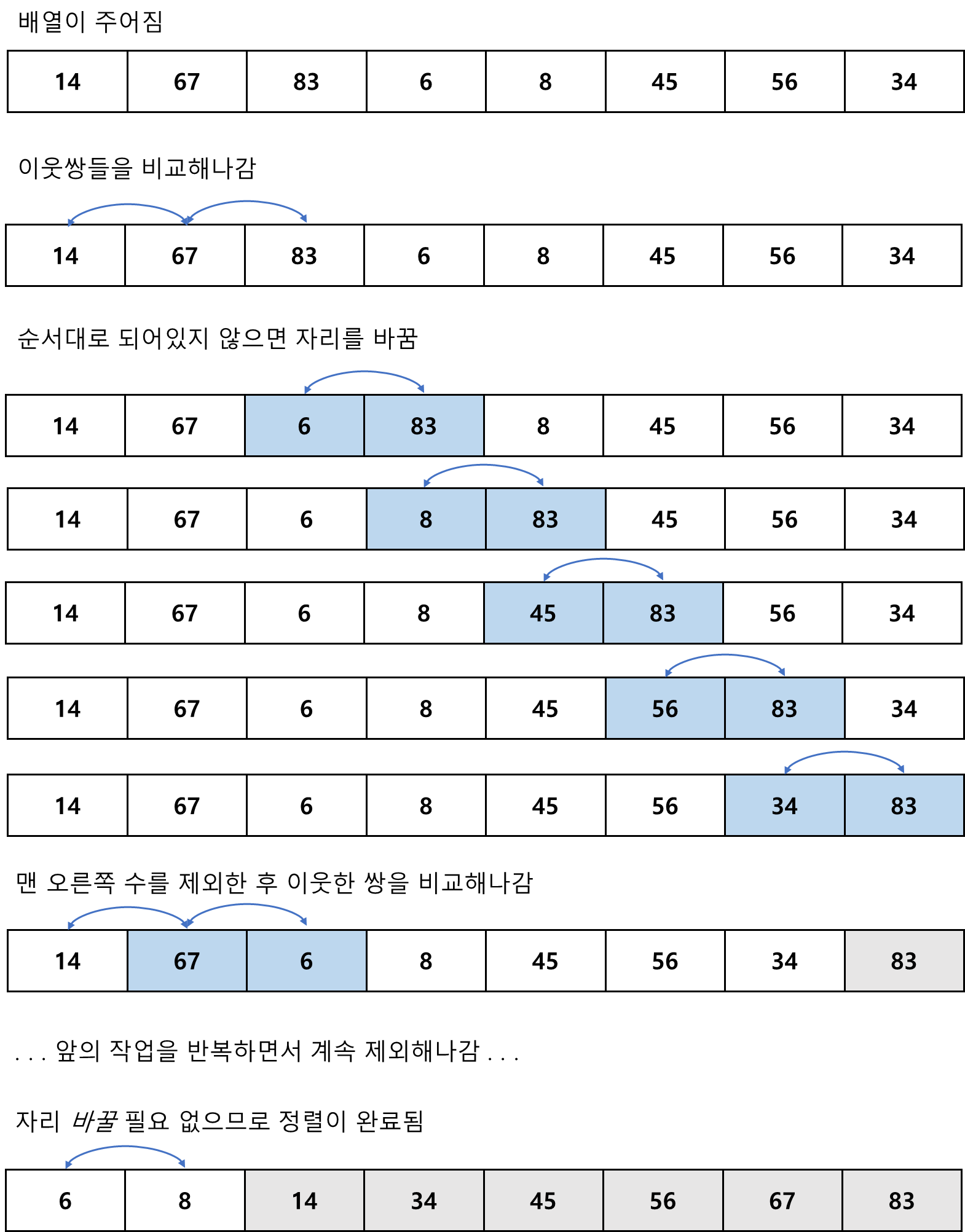
- 선택 정렬처럼 제일 큰 원소를 끝자리로 옮기는 작업을 반복함.
- 다만 제일 큰 원소를 오른쪽으로 옮기는 방법이 다름.
bubbleSort(A[],n)
{
① for last <- n downto 2
② for i <- 1 to last -1
③ if (A[i] > A[i+1] ) then A[i] <->A[i+1]; // 원소 교환
}
- 알고리즘은 크게 두 개의 for 루프로 구성되어 있음. 첫 번째 for 루프, ①의 for 루프는 선택 정렬의 for 루프와 역할이 똑같음.
- 루프를 돌 때마다 제일 큰 원소를 맨 오른쪽으로 보내고 정렬할 배열의 크기를 하나씩 줄임.
- 안쪽의 for 루프, ②의 for 루프는 가장 큰 원소를 맨 오른쪽으로 보내는 것임. -> 이 부분이 선택 정렬과 다름.
- 버블 정렬은 이웃한 수를 비교하면서 순서가 제대로 되어 있지 않으면 하나하나 바꾸어나감.
버블 정렬의 수행 시간
- ①의 for 루프는 선택 정렬에서처럼 n-1번 순환함.
- ②의 for 루프는 last-1번 순환함. last가 n에서 2까지 1씩 감소하므로 ②의 for루프가 총 순환하는 횟수는 n(n-1)/n임.
- 이것이 알고리즘의 시간을 좌우함.
- ③은 상수 시간 작업임.
∴ 버블 정렬의 수행 시간은 θ(n²)
- 앞서 나온 알고리즘은 수행을 시작할 때나 중간에 배열이 이미 정렬이 되어 있는 상태라도 계속 끝까지 무의미한 순환을 계속함. 이를 위해 알고리즘에 한가지 장치를 하는 방법이 있음.
bubbleSort(A[],n)
{
① for last <- n downto 2 {
sorted <-True;
② for i <- 1 to last -1
if (A[i] > A[i+1] ) then {
A[i] <->A[i+1]; // 원소 교환
sorted <- FALSE;
}
}
③ if (sorted = TRUE) then return;
}
- ②의 for 루프가 시작되기 직전에 매번 sorted라는 표식자를 TRUE로 설정해두고, 이것이 ②의 for루프를 도는 동안 변하는지 봄.
- 중간에 한번이라도 A[i] <->A[i+1]의 교환이 일어나면 이것은 FALSE로 바꿈.
- ②의 루프를 도는 동안 한 번도 교환이 일어나지 않으면 배열은 이미 정렬되어 있는 상태임.
- 이때는 ③에서 리턴함으로써 알고리즘을 끝내버리면 됨.
- 이렇게 되면 정렬된 배열이 입력되면 ①의 for 루프를 첫 첫번째 순환하고 리턴하여 끝남.
- θ(n)의 시간이 소요됨.
삽입 정렬
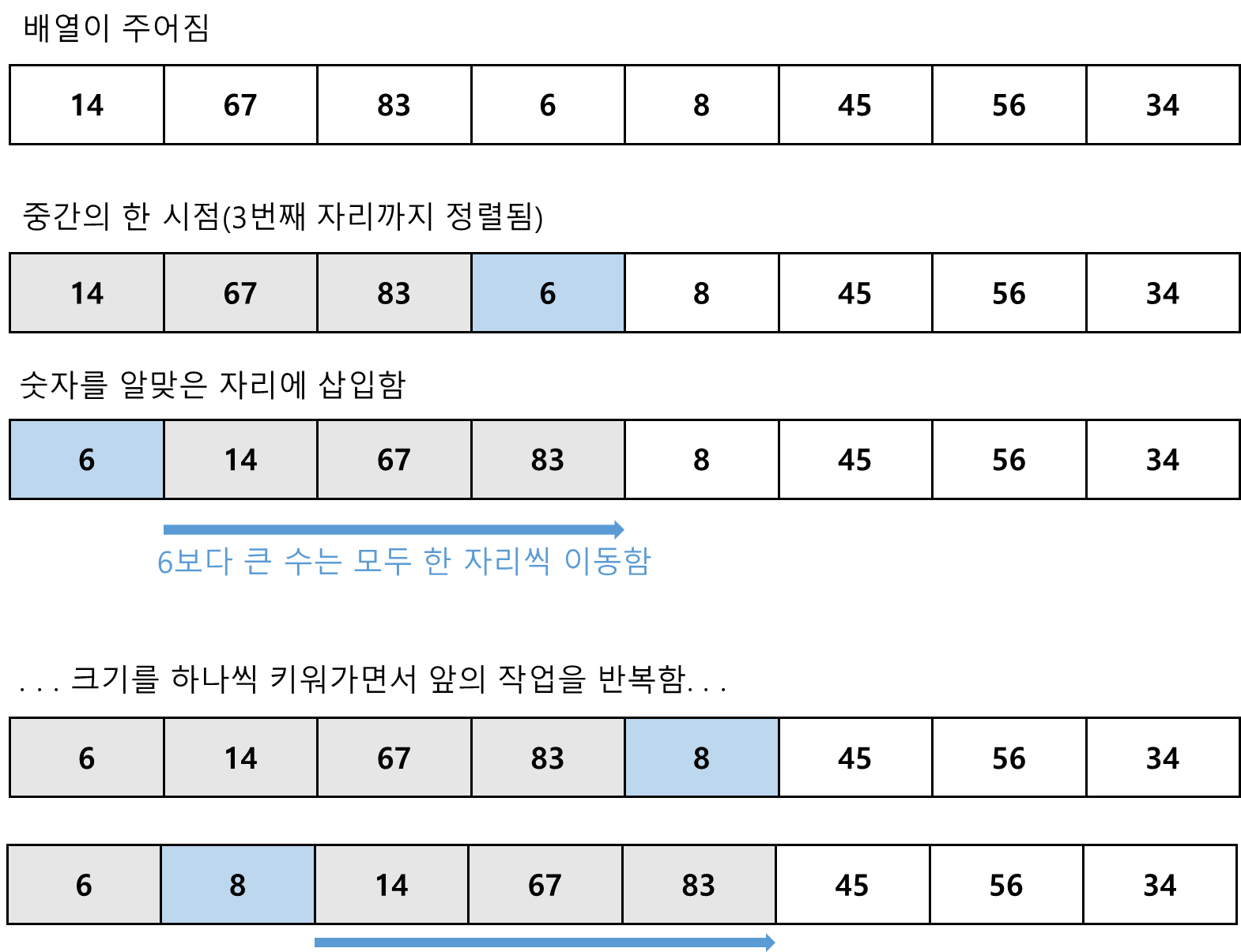
- 이미 정렬되어 있는 i개짜리 배열에 하나의 원소를 더 더하여 정렬된 i+1개짜리 배열을 만드는 과정을 반복함.
- 선택 정렬과 버블 정렬이 n개짜리 배열에서 시작하여 그 크기를 하나씩 줄이는 데 반하여, 삽입 정렬은 한 개짜리 배열에서 시작하여 그 크기를 하나씩 늘리는 정렬임.
insertionSort(A[],n)
{
① for i <- 2 to n
② A[ 1 ~ i ]의 적합한 자리에 A[i]를 삽입함;
}
- ①의 for 루프는 문제의 크기를 하나씩 키워나가는 역할을 함.
- ②를 수행하기 직전 시점에 A[1 ~ i-1]은 항상 정렬이 되어 있음.
- ②를 수행하고 나면, A[i]까지 정렬이 됨. 즉, 이미 정렬된 배열과 원소 A[i]를 받아 정렬된 배열을 만듦. A[i]가 정렬된 배열의 원소보다 크면 제자리에 두고 그렇지 않으면 하나씩 탐색하며 A[i]가 들어갈 자리를 찾음. 그 자리 이후의 원소들은 한 칸씩 오른쪽으로 밀려나게 됨.
삽입 정렬의 수행 시간
- ①의 for 루프는 n-1번 순환함.
- 매 for 루프에서 ②의 while 루프는 최대 i-1번 순환함.
- 가장 운이 나쁠 경우 i-1번의 순환이 필요하고, 가장 운이 좋으면 A[i]가 제자리에 있게 되어 while 루프는 한 번도 수행하지 않음.
- 최악의 경우 수행시간은 θ(n²)
- 삽입 정렬은 O(n²) 시간이 드는 비효율적인 정렬 알고리즘군에 속하지만 배열이 거의 정렬되어 있는 상태로 입력되는 경우에는 효율적임.
- 배열이 정렬된 상태로 입력되면 ②의 while 루프는 수행되지 않아 상수 시간이 소요되고, for 루프는 n-1번 순환되므로 θ(n)의 시간이 들게 됨. 거의 정렬이 되어 있을 때도 ②의 삽입이 수월해져 θ(n)에 가까운 시간이 들게 됨.
2. 고급 정렬 알고리즘
병합 정렬
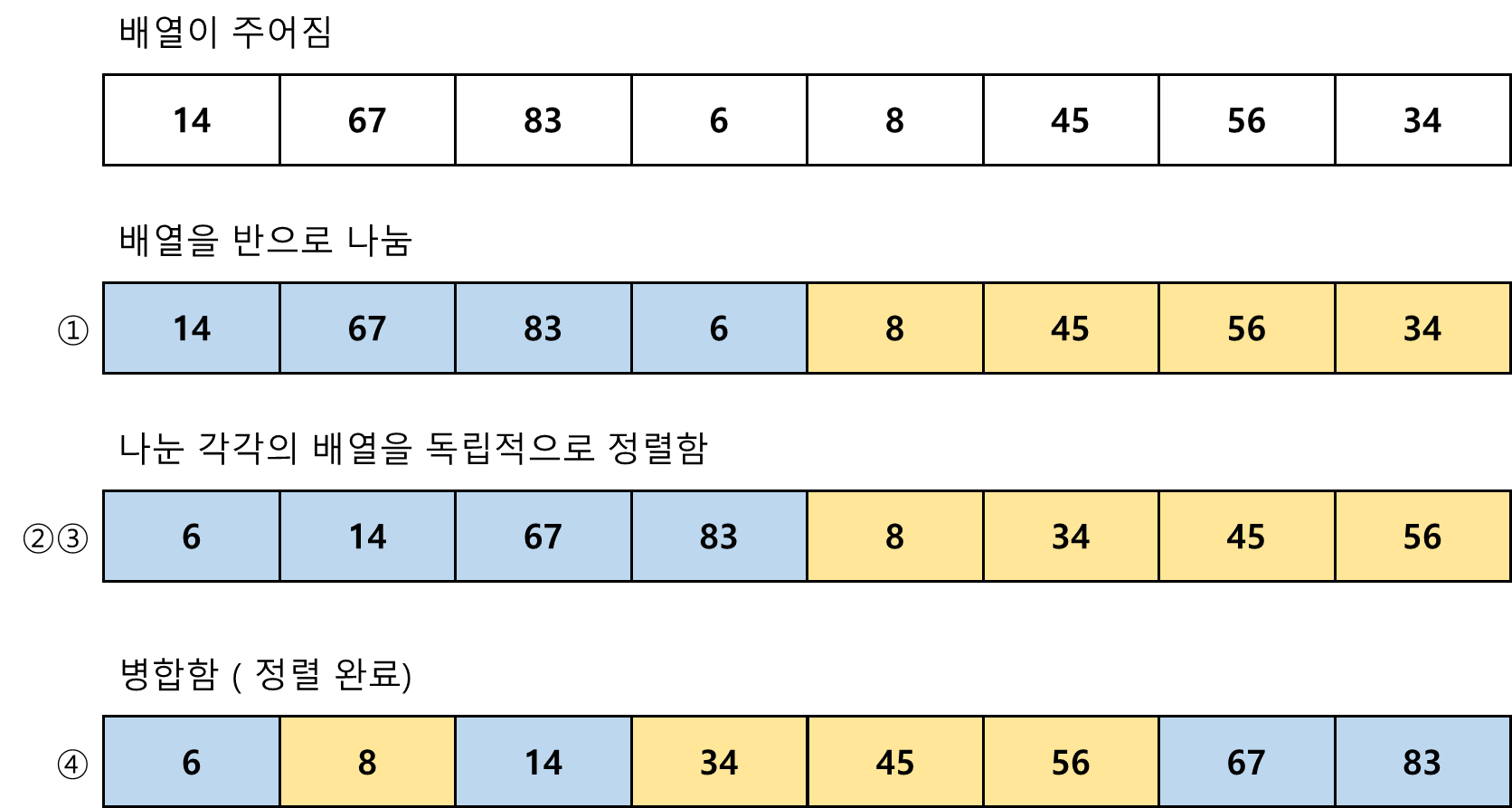
- 병합 정렬은 입력을 반으로 나눈 후 전반부와 후반부를 각각 독립적으로 정렬함.
- 마지막으로 정렬된 두 부분을 합쳐서 정렬된 배열을 얻음.
- 여기서 전반부나 후반부를 정렬할 때도 반으로 나눈 다음 정렬해서 병합함. (재귀적으로 반복함)
mergeSort(A[], p, r) // A[p ~ r]을 정렬함
{
if ( p < r ) then {
① q <- (p+r)/2; // p, r의 중간 지점 계산
② mergeSort(A,p,q); // 전반부 정렬
③ mergeSort(A,q+1,r); // 후반부 정렬
④ merge(A,p,q,r); // 병합
}
}
merge(A[],p,q,r)
{
정렬되어 있는 두 배열 A[p~q]와 A[q+1 ~ r]을 합쳐
정렬된 하나의 배열 A[p ~ r]을 만듦.
}
병합 정렬의 수행 시간
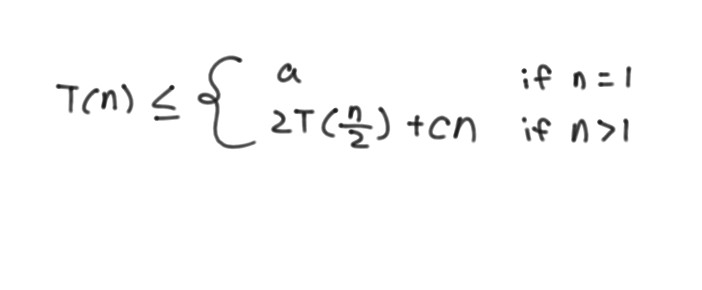
- 여기서 상수 a는 크기는 1인 문제를 푸는 시간을 나타냄.
- 상수 c는 병합에 드는 시간을 충분히 잡아주기 위해 n에 곱함. 비교의 횟수만으로 수행 시간을 분석한다면 c=1로 충분함.
- 병합은 선형 시간이 소요됨. 여기서 T(n/2)은 두 개의 작은 문제를 처리하는 비용, 즉 재귀적 호출과 관련된 비용.
- 병합 정렬의 수행 시간은 최악의 경우 θ(n logn)이 됨.
퀵 정렬
- 퀵 정렬은 평균적으로 가장 좋은 성능을 가져 현장에서 가장 많이 쓰는 정렬 알고리즘
- 한 원소를 기준으로 삼고 기준보다 작은 수는 기준의 왼쪽에, 나머지는 기준의 오른쪽에 오도록 재배치하여 독립적으로 정렬함.
- 왼쪽과 오른쪽의 정렬을 위해 다시 퀵 정렬을 사용함.

quickSort(A[], p, r)
{
① if ( p < r ) then {
② q <- partition(A, p, r); // 분할
③ quickSort(A, p, q-1); // 왼쪽 부분 배열 정렬
④ quickSort(A, q+1, r); // 오른쪽 부분 배열 정렬
}
}
partition(A[], p, r)
{
배열 A[p ~ r]의 원소들을 A[r]을 기준으로 양쪽으로 재배치하고 A[r]이 자리한 위치를 리턴함;
}
- 기준원소를 중심으로 양쪽으로 나누고 나서② 두개의 퀵 정렬을 재귀적으로 호출하고 있음.(③,④)
- 병합 정렬은 먼저 재귀적으로 작은 문제를 해결한 다음 후처리를 하는데 반해, 퀵 정렬은 선행 작업을 한 다음 재귀적으로 작은 문제를 해결하면서 바로 끝냄.
힙 정렬
- 힙 정렬은 힙이라는 특수한 자료구조를 사용하는 정렬 알고리즘
- 힙은 최소합과 최대힙이 있는데 값이 저장되는 방향만 반대일 뿐 성질은 똑같음.
힙
- 힙은 이진 트리로서 맨 아래 층을 제외하고는 완전히 채워져 있고 맨 아래층은 왼쪽부터 꽉 채워져 있음.
- 힙의 모든 노드는 하나씩의 값을 갖고 있는데 "각 노드의 값은 자기 자식의 값보다 작다(힙에 값이 같은 원소가 두 개 이상 있는 경우에는 "작다" 대신 "작거나 같다")."는 힙성질을 만족함.
- 리프 노드는 자식이 없으므로 자동 만족됨.
- 모든 노드가 이 성질을 만족하면, 이진 트리의 루트 노드에는 최솟값이 자리하게 됨.
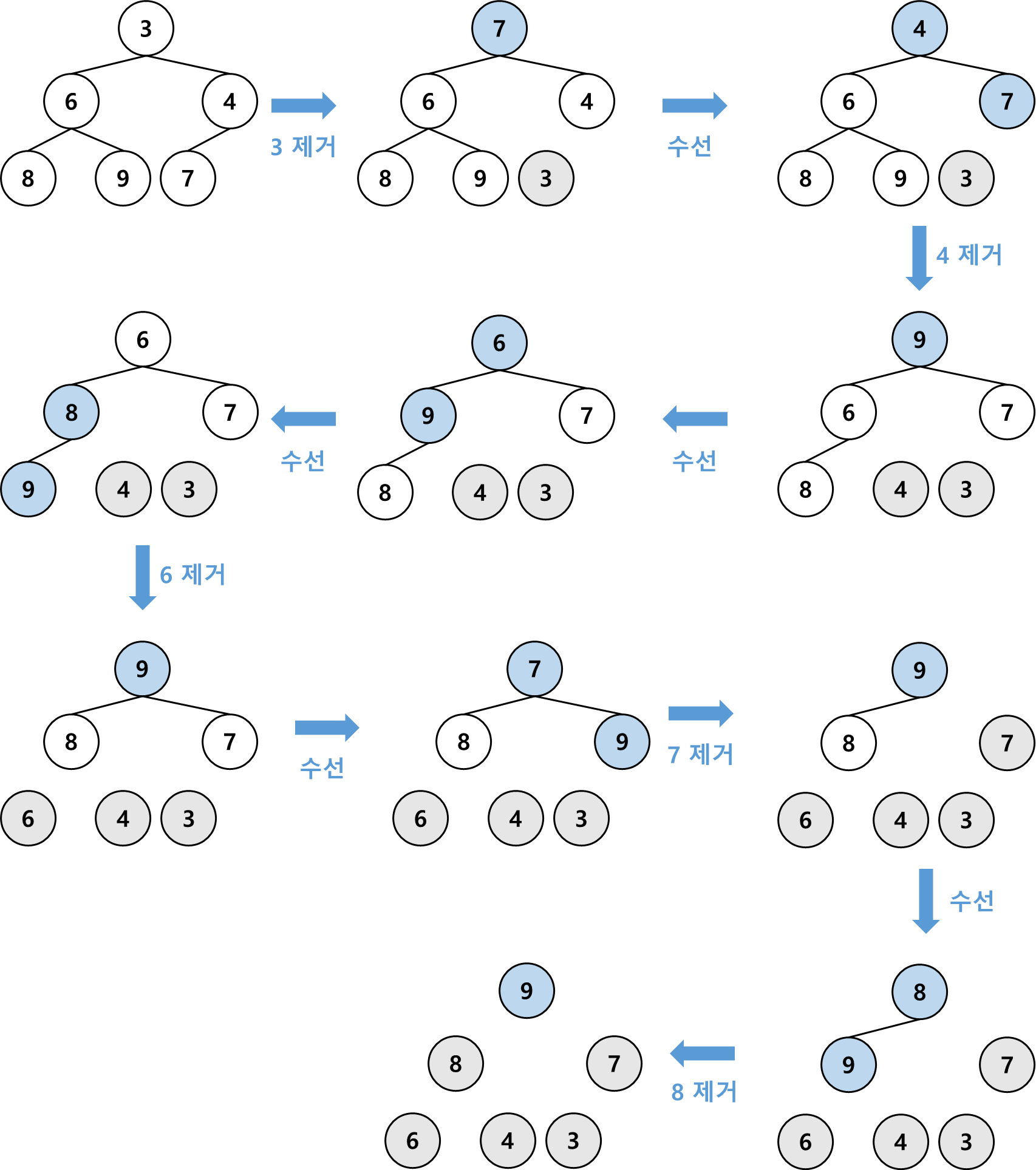
힙 정렬
- 루트 노드에 있는 원소를 제거하여 다른 곳에 저장함.
- 루트 노드가 없어졌으므로 트리의 크기가 하나 줄게됨. 맨 끝에 있는 원소를 루트 노드에 옮겨 새로운 루트로 삼음.
- 이것으로 대부분의 경우 루트 노드와 자식 간에 힙성질이 깨짐.
- 힙성질이 깨지면 수선을 함.
- 이를 반복하면 역순으로 정렬됨.
heapSort(A, n)
{
buildHeap(A, n);
① for i <- n downto 2 {
A[1] <-> A[i]; // 원소 교환
heapify(A, 1, i-1);
}
}
heapify(A[], k, n) // A[k]를 루트로 하는 트리를 힙성질을 만족하도록 수선함. n은 최대 인덱스( 전체 배열의 크기)
{
left <- 2k; right <- 2k+1;
// 작은 자식 고르기.
if ( right <= n ) then { // k가 두 자식을 가지는 경우
if ( A[left] < A[right] ) then smaller <- left;
else smaller <- right;
}
else if (left <= n ) then smaller <-left; // k가 왼쪽 자식만 있는 경우
else return;
//재귀적 조정
if (A[smaller] < A[k] ) then {
A[k] <-> A[smaller];
heapify(A,smaller,n);
}
}
수행 시간
- buildHeap()은 θ(n)의 시간이 듦.
- ①의 for 루프는 n-1번 순환하고 각 순환에서 시간을 좌우하는 heapify()는 충분히 잡아서 O(log n)의 시간이면 됨.
- 그러므로 힙 정렬의 총 수행 시간은 O(n log n)임.
3. 비교 정렬 시간의 하한
- 정렬 알고리즘들의 공통점은 원소끼리 비교하는 것으로만 정렬을 한다는 것. 이런 정렬을 통칭해 비교 정렬이라 함.
- 비교 정렬은 최악의 경우 수행시간이 절대 Ω(n log n)을 밑돌 수 없음. 이것은 결정 트리 모델을 사용해서 증명할 수 있음.
a1 < a2?의 비교 결과 a1<a2이면 왼쪽으로 이동하고 그렇지 않으면 오른쪽으로 이동함.
- 이런 식으로 리프 노드를 만날 때까지 반복함.
- 정렬 알고리즘은 입력 수열의 모든 가능한 경우에 대해 다 제대로 정렬을 해주어야 하므로 결정 트리의 리프 노드는 n!개가 되어야함. 이는 θ(n log n)
- 최악의 경우는 결정 트리에서 가장 깊은 리프 노드까지 내려가는 것.
- n!개의 리프 노드를 가진 트리의 높이는 적어도 log₂ n!임.
- 최악의 경우 수행 시간은 Ω(n log n)
4. 특수 정렬 알고리즘
기수 정렬
- 기수 정렬은 입력이 모두 k 자릿수 이하의 자연수인 특수한 경우에 사용할 수 있는 방법으로 θ(n) 시간이 소요되는 정렬 알고리즘임.
- 가장 낮은 자릿수만 가지고 모든 수를 재배열함. 그 다음 가장 낮은 자릿수는 잊어버림. 그리고 앞과 같은 방법으로 더 이상 자릿수가 남지 않을 때까지 계속함.
radixSort( A[], n, k)
// 원소들이 각각 최대 k자릿수인 A[1 ~ n]을 정렬함.
// 가장 낮은 자릿수를 1번째 자릿수라 함.
{
for i <- 1 to k
① i번째 자릿수에 대해 A[1 ... n ]을 안정성을 유지하면서 정렬함;
}
- 값이 같은 원소끼리는 정렬 후에 원래의 순서가 바뀌지 않는 성질을 뜻함.
- ①에서 기존의 정렬 알고리즘을 쓴다면 그것만으로 θ(n) 시간을 초과해버리므로 다른 방법을 사용해야함.
계수 정렬
- 계수 정렬은 정렬하고자 하는 원소들의 값이 O(n)을 넘지 않는 경우에 사용할 수 있음.
- 배열 A[1 ~ n]의 원소들이 k를 넘지 않는 자연수인 경우를 들 수 있음.
- 계수 정렬은 먼저 배열의 원소를 훑어보고 1부터 k까지의 자연수가 각각 몇 번 나타나는지를 셈.
- 이 정보가 있으면 A[1 ~ n]의 각 원소가 몇 번째에 놓이면 되는지 계산해낼 수 있음.
countingSort(A[], B[], n)
// A[1 ~ n] : 입력 배열
// B[1 ~ n] : 배열 A[]를 정렬한 결과
{
① for i <- 1 to k
C[i] <- 0;
② for j <- 1 to n
C[A[j]]++;
// 이 시점에서 C[i] : 값이 i인 원소의 총수
③ for i <- 2 to k
C[i] <- C[i] + C[i-1];
// 이 시점에서 C[i] : i보다 작거나 같은 원소의 총수
④ for j <- n downto 1 {
B[C[A[j]]] <-A[j];
C[A[j]]--;
}
}
- ②의 for 루프에서 배열 C[1 ~ k]에 자연수 1부터 k 각각이 배열 A에서 몇 번 나타나는지 세어둠. C[i]가 값이 i인 원소의 원소의 총수를 갖고 있게 됨.
- ③의 for 루프에서 C[i]가 값이 i보다 작거나 같은 원소의 총수를 갖고 있도록 바꿈.
- 마지막으로 ④의 for 루프에서 이 정보를 이용해 배열 A의 각 원소가 배열 B의 몇 번째 자리에 들어갈지 판단하여 저장함.
- 계수 정렬의 수행 시간은 θ(n)
'개인 공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 검색 트리 (0) | 2023.02.11 |
|---|---|
| [알고리즘] 선택 알고리즘 (0) | 2023.02.10 |
| [알고리즘] 점화식과 알고리즘 복잡도 분석 (0) | 2023.02.08 |
| [알고리즘] 알고리즘 설계와 분석의 기초 (0) | 2023.01.31 |
| [알고리즘] 알고리즘이란 (0) | 2023.01.30 |


