- Image_classification
- programmers
- SingleProject
- cloud_computing
- Kubernetes
- 티스토리챌린지
- Java
- Python
- Artificial_Intelligence
- datastructure
- kubeflow
- 리눅스마스터2급
- Univ._Study
- Operating_System
- tensorflow
- 오블완
- Android
- 자격증
- Algorithm
- Personal_Study
- 2023_1st_Semester
- Linux
- Database_Design
- C
- Baekjoon
- codingTest
- c++
- app
- Unix_System
- study
코딩 기록 저장소
[알고리즘] 해시 테이블 본문
1. 해시 테이블 : 검색 효율의 극단
- 검색 트리는 원소가 저장될 자리가 이미 트리에 존재하는 원소와 비교하여 결정되는 반면, 해시 테이블은 원소가 저장될 자리가 원소의 값에 의해 결정되는 자료구조.
- 저장된 자료와 비교하여 자리를 찾지 않고 단 한 번의 계산으로 자신의 자리를 찾음.
- 임의의 원소를 해시 테이블에 저장하려면 먼저 해당 원소의 해시 값을 계산 함.
- 해시 값은 해시 함수로 계산됨.
- 해시 테이블이 총 m개의 원소를 저장할 수 있다면 테이블의 각 자리는 0부터 m-1의 주소 값을 갖고, 해시 함수는 임의의 원소 값을 입력으로 받아 0,1,2, ... , m-1 중의 한 값을 리턴함.
- 이 리턴 값이 바로 해당 원소를 저장하는 주소.
- 가장 간단한 방법은 원소 값이 x라면 x를 m으로 나눈 나머지를 해시 값으로 삼는 것.
25, 13, 16, 15, 7을 차례로 저장한 예

2. 해시 함수
- 해시 함수는 키 값을 입력으로 받아 해시 테이블상의 주소를 리턴함.
- 해시 함수는 다음 두가지 성질을 가지도록 만들어야 함.
1. 입력 원소가 해시 테이블 전체에 고루 저장되어야 함.
2. 계산이 간단해야 함.
- 첫번째 성질이 중요함. 이 성질을 만족해야 서로 다른 두 원소가 한 주소를 놓고 충돌할 확률이 작아지기 때문.
- 첫 번째 성질을 만족하기 위해 해시 함수에 지나치게 복잡한 계산이 필요한 경우는 없음.
- 두 번째 성질은 대부분 신경 쓰지 않아도 쉽게 만족됨.
나누기 방법
h(x) = x mod m
- 위와 같은 모양의 해시 함수
- 여기서 m은 해시 테이블의 크기. 해시 테이블에 있는 m개의 자리가 0부터 m-1의 주소 값을 가지므로 m으로 나눈 나머지 연산을 사용하는 것이 매우 자연스러움.
- 해시 테이블 크기 m은 2의 멱수에 가깝지 않은 소수를 택하는 것이 좋음.
- 만일 m=2^p이라면 입력 원소의 하위 p비트에 의해 해시 값이 결정되므로 해시 값을 분산시키기에 이상적이지 않음.
- 해시 값은 입력 원소의 모든 비트를 이용하는 것이 확률적으로 좋은 분포를 갖도록 하는 데 유리함.
곱하기 방법
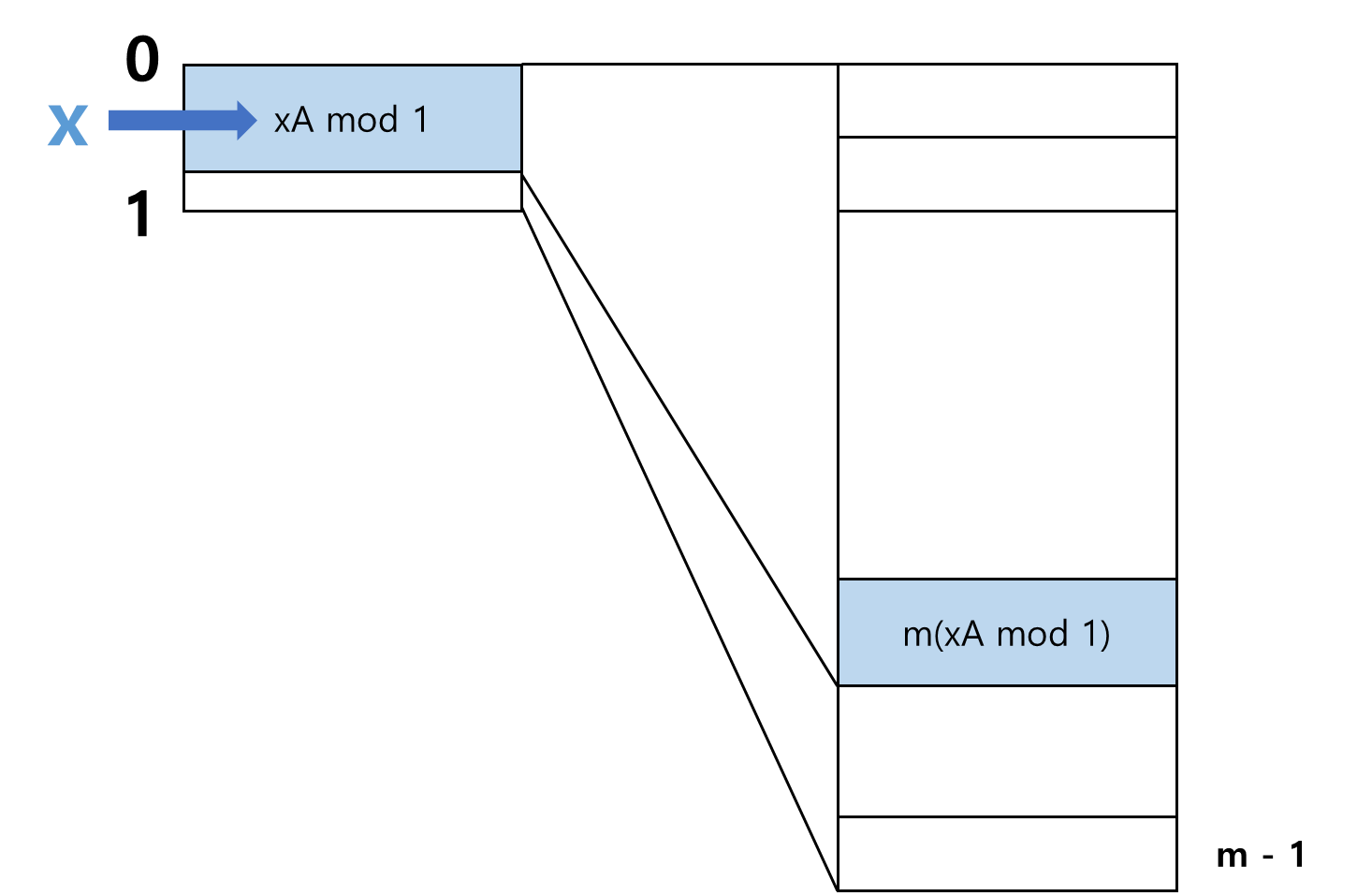
h(x) = m(xA mod 1)
- 나누기 방법은 해시 테이블의 크기보다 큰 수를 해시 테이블 크기 범위에 들어오도록 수축시킴.
- 곱하기 방법은 이와 반대.
- 곱하기 방법에서는 먼저 입력값을 0과 1 사이의 소수로 대응시킨 다음 해시 테이블 크기 m을 곱하여 0부터 m-1 사이로 팽창시킴.
- 이 방법에서는 해시 함수의 특성을 결정짓는 0 < A < 1 범위의 상수 A를 미리 준비해 놓아야 함.
- 임의의 원소 x에 대해 다음 과정을 거쳐 x의 주소를 결정함.
1. x에 A를 곱한 다음 소수부만 취함.
2. 방금 취한 소수부에 m을 곱하여 그 정수부를 취함.
- 곱하기 방법은 나누기 방법과는 달리 해시 테이블의 크기 m을 아무렇게나 잡아도 상관없음.
- 따라서 컴퓨터의 이진수 환경에 맞게 m=2^p으로 잡는 것이 자연스러움.
- 대신 상수 A를 어떻게 잡느냐에 따라 해시 값 분포가 많은 영향을 받음.
- 크누스[97]는 잘 작동하는 A값으로 루트 5 -1 / 2인 0.6180339887 . . . 을 제안함.
3. 충돌 해결
- 해시 테이블 내의 한 주소를 놓고 두 개 이상의 원소가 자리를 다투는 것을 충돌이라고 함.
- 한 원소를 해싱해서 저장하려는데 다른 원소가 이미 그 자리를 차지한 상황을 뜻함.
- 충돌 해결 방법에는 체이닝, 개방 주소 방법 등 두가지 방법이 있음.
체이닝
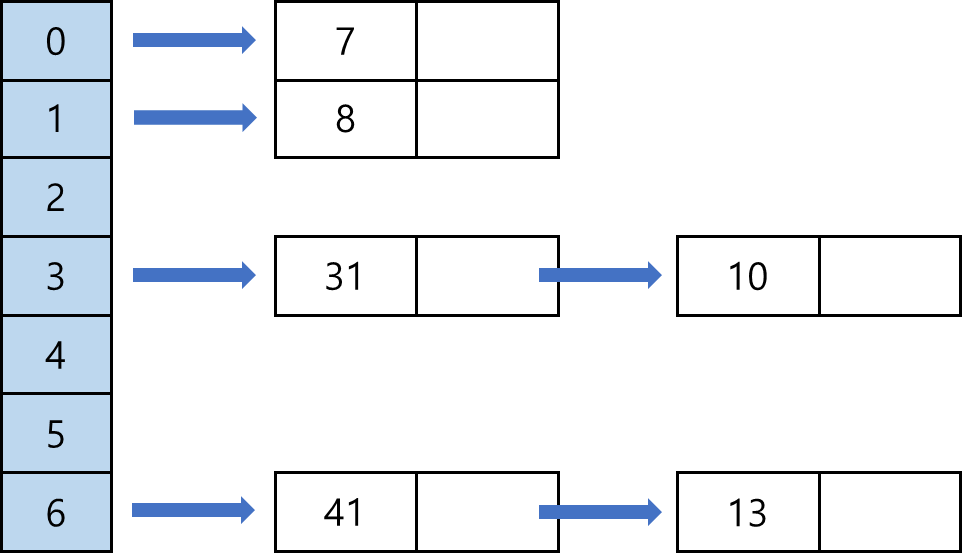
- 해시 테이블의 각 주소가 리스트의 헤더 역할을 하고, 여기에 해당 주소로 들어오는 원소들이 연결 리스트로 매달림.
- 해시 테이블 크기가 m이면 최대 m개의 연결 리스트가 존재할 수 있음.
- 체이닝은 적재율이 1을 넘어도 사용할 수 있는 장점이 있음.
체이닝을 사용한 해시 테이블의 알고리즘
chainedHashInsert( T[], x ) // T : 해시 테이블, x : 삽입 원소
{
리스트 T[h(x)]의 맨 앞에 x를 삽입;
}
chainedHashSearch( T[], x )
{
리스트 T[ h(x) ]에서 x값을 가지는 원소를 검색;
}
chainedHashDelete( T[], x)
{
리스트 T[ h(x) ]에서 x의 노드를 삭제;
}
개방 주소 방법
- 개방 주소 방법은 체이닝과 같은 추가 공간을 허용하지 않음.
- 충돌이 일어나더라도 어떻게든 주어진 테이블 공간에서 해결함.
- 모든 원소가 반드시 자신의 해시 값과 일치하는 주소에 저장된다는 보장은 없음.
임의의 원소를 해시 테이블에 삽입하는 과정
- 먼저 해시 함수를 계산함.
- 계산된 주소를 차지하고 있는 다른 원소가 없으면 그 자리에 넣음.
- 그 자리에 다른 원소가 있으면 충돌이 일어난 것.
- 정해진 규칙에 따라 다음 자리를 찾는데 빈자리를 찾을 때까지 계속 찾음.
- 이것을 순차적인 해시 함수로 볼 수 있음.
- 즉 처음 계산한 해시 함수를 0번째 해시 함수, 충돌이 일어나서 다음 주소를 계산하는 것을 1번째 해시 함수, 식으로 볼 수 있음.
- 다음 주소를 정하는 방법도 다양함.
1. 선형 조사
- 가장 간단한 충돌 해결 방법으로 충돌이 일어난 바로 뒷자리를 보는 것.
- 충돌이 일어난 자리에서 i에 관한 일차 함수의 보폭으로 이동하는 것.
- hi(x)는 h(x)에서 i만큼 떨어진 자리가 됨.
- 테이블의 경계를 넘어갈 경우에는 맨 앞으로 가면 됨.
hj(x) = (h(x) + i)mod m // i = 0, 1, 2, ...
- 선형 조사의 경우 특정 영역에 원소가 몰릴 때는 치명적으로 성능이 떨어짐.
- 이런 현상을 1차 군집이라 함.
2. 이차원 조사
- 바로 뒷자리를 보는 대신에 보폭을 이차 함수로 넓혀가면서 봄.
- i번째 해시 함수를 h(x)에서 i²만큼 떨어진 자리로 삼을 수 있음.
- 즉, h(x), h(x) +1, h(x)+4, h(x) + 9, h(x) + 16과 같이 볼 수 있음.
h(x) = ( h(x) + c1 i² + c2 i) mod m // i = 0, 1, 2, ...
- 이렇게 하면 선형 조사에서처럼 특정 영역에 원소가 몰려도 그 영역을 빨리 벗어날 수 있음.
- 그러나 여러 개의 원소가 동일한 초기 해시 함수 값을 갖게 되면 모두 같은 순서로 조사를 할 수 밖에 없어 비효율적이 됨.
- 이런 현상을 2차 군집이라 함.
3. 더블 해싱
hi(x) = ( h(x) + i f(x)) mod m // i = 0, 1, 2 ...
- 여기서 h(x)와 f(x)는 서로 다른 해시 함수.
- 이 방법에서는 충돌이 생겨 다음에 볼 주소를 계산할 때 두 번째 해시 함수 값만큼씩 점프함.
- 두 원소의 첫 번째 해시 값이 같더라도 두 번째 함수 값이 같을 확률은 매우 작으므로 서로 다른 보폭으로 점프를 하게 됨.
- 두 개의 해시 함수를 정할 때 권장하는 방법은 h(x) = x mod m으로 잡고, m보다 조금 작은 소수 m'에 대해 f(x) = 1 + (x mod m')으로 잡는 것.
- 조심할 점 : 두 번째 해시 함수 값 f(x)가 해시 테이블 크기 m과 서로 소인 값이어야 한다는 것.
개방 주소 방법의 알고리즘
hashInsert(T[], x)
{
i <- 0;
repeat {
j <- hi(x);
if ( T[j] = NIL or T[j] = DELETED )
then { T[j] <- x; return j;}
else i++;
} until ( i = m )
error "테이블 오버플로";
}
hashSearch(T[], x)
{
i <- 0;
repeat {
j <- hi (x);
if ( T[j] = x )
then return j
else i ++;
} until ( T[j] = NIL or i = m )
return NIL;
}
- 개방 주소 방법은 테이블에 주어진 공간만 사용할 수 있으므로 적재율이 1을 넘을 수는 없음.
- 적재율이 높아지면 효율이 급격히 떨어지므로 적당한 임계점을 설정한 후 그것을 넘으면 해시 테이블의 크기를 대략 두 배로 키우고 모든 원소를 다시 해싱하는 것이 일반적임.
- 삭제할 때는 주소 자리에 DELETED라는 상수 값을 저장하여 삭제된 자리라는 것을 표시함.
4. 해시 테이블에서 검색 시간 분석
- 이론적으로는 체이닝이 개방 주소 방법보다 평균 조사 횟수가 적음.
- 개방 주소 방법의 경우 자신과 직접 충돌을 일으키지 않은 원소라도 검색 과정에 방해를 할 수 있음.
- 충돌이 일어나면 자신의 해시 값이 아닌 다른 주소에 어떻게든 자리를 잡기 때문.
- 체이닝은 충돌을 일으킨 원소만 같은 연결 리스트에 매달려 검색에 지장을 주진 않지만, 각 연결 리스트마다 헤드를 하나씩 두어야 하고 연결 리스트를 만들기 위해 각 원소마다 연결 공간이 필요함.
- 적재율이 그리 높지 않을 때는 개방 주소 방법이 더 매력적임.
'개인 공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 동적 프로그래밍 (1) | 2023.02.18 |
|---|---|
| [알고리즘] 집합의 처리 (1) | 2023.02.17 |
| [알고리즘] 검색 트리 (0) | 2023.02.11 |
| [알고리즘] 선택 알고리즘 (0) | 2023.02.10 |
| [알고리즘] 정렬 (0) | 2023.02.08 |




